Plotting the radial wave function of Deuteron in a finite well

[TopologyisGeometry]

Homework Statement

Plot the wave function $u(r)$ as a function of $r$ from 0 to 10 fm. Since $u$is not normalized, you won't need units on the y axis.

Relevant Equations

$$\frac{-\hbar^2}{2\mu}\frac{d^2u(r)}{dr^2}+V(r)u(r) = Eu(r)$$ Where $$V(r) = \begin{cases}-V_0 \quad r<R\\ 0\quad r>R\end{cases}$$ Which has the solutions previously found to be

$$u(r)=\begin{cases}A\sin(kr)\quad r<R\\ De^{-\kappa r}\qquad r>R\end{cases}$$

To plot $u(r)$ we need to find the solutions for each region. Which is in the relevant equations part. Now, I have to do this numerically. Using python 3.7 I made an $u$ which is filled with zeros and a for loop with if/elseif statement, basically telling it to plot values for whenever $r<R$ and $r>R$. Here is the plot generated by my simple code

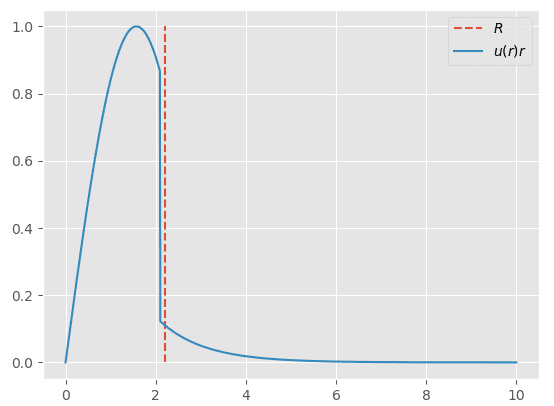
Due to continuity at $r=R$ they need to have the same value. Which makes me believe that this is a root finding problem, basically $A\sin(kr)-De^{-\kappa r}=0$ Now I don't know how to implement this onto my code, at first I thought make another elif statement for when $r==R$ to use the roots as the values, how would I go on about this problem? Have I forgotten something?

 

[kuruman]

You have some prepping to do that it is better done with pencil and paper, not code. At $r=R$, the wavefunction and its derivative must be continuous. This will give you a relation between $k$ and $\kappa$ which you will have to solve numerically (the root finding part) to find $k$ and $\kappa$ for an assumed numerical value of $V_0.$ Then you can write the unnormalized wavefunction in terms of $A$ or $D$ and plot.

 

[TopologyisGeometry]

You have some prepping to do that it is better done with pencil and paper, not code. At $r=R$, the wavefunction and its derivative must be continuous. This will give you a relation between $k$ and $\kappa$ which you will have to solve numerically (the root finding part) to find $k$ and $\kappa$ for an assumed numerical value of $V_0.$ Then you can write the unnormalized wavefunction in terms of $A$ or $D$ and plot.

I found that $k\cot{kr} = -\kappa$ which comes from the fact that we claim $u(r)$ to be continuous everywhere and it's derivate too, then I just divided to get rid of the coefficients, where $k^2=2\mu(E+V0)/\hbar^2$ and $\kappa^2=2\mu E/\hbar^2$ if that's what you're asking $V0=35MeV$ and I found that $E=-2.223 MeV$ This should be everything to plot this right?

 

[kuruman]

Before plotting, I would evaluate $u(r)$ and its derivative at $r=R$ to make sure that I did not make any mistakes. Also, if you are not going to normalize $u(r)$, be sure to use one of the continuity equations in order to write $u(r)$ in terms of single constant, $A$ or $D$.