Points of inflection on acceleration graph

[member 731016]

Homework Statement

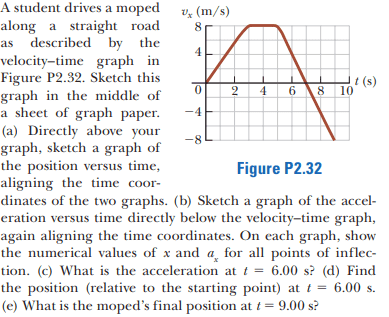
Please see below

Relevant Equations

Please see below

EDIT: For this part(b) of this problem,

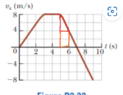
The solution is

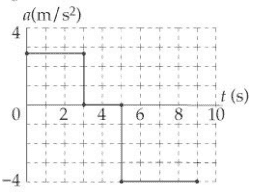
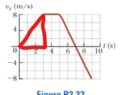
However, isn't there more points of inflection than just $t = 3,5 s$? Points of inflection is when $x'' = a = 0$ so it should be $3 ≤ t ≤ 5 s$

I also have a question about part(d):

The solution is

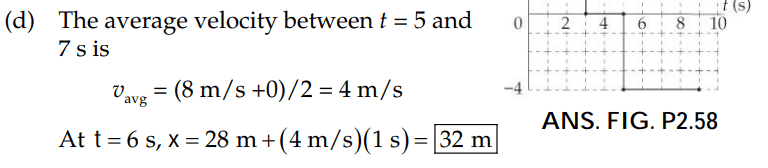
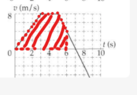
However, could I tried solving for the position by finding the area under the velocity curve from t = 0 to t = 6 sec.

$0.5 \times 3 \times 8 + 2 \times 8 + 1\times 4 + 1 \times 1 \times 4 = 34 m$.

I don't understand what I have done wrong since I should be able to get the correct answer from areas.

Can someone please help?

Many thanks!

 

[haruspex]

$0.5 \times 2.5 \times 8 = 10 m$

2.5? Look again.

 

[member 731016]

2.5? Look again.

Thank you for your reply @haruspex! Do you please know the answer to my new confusion?

Many thanks!

 

[haruspex]

isn't there more points of inflection than just t=3,5s?

It should not refer to inflection points here. The first and second derivatives of v would need to exist and be continuous.

$0.5 \times 3 \times 8 + 2 \times 8 + 1\times 4 + 1 \times 1 \times 4 = 34 m$.

For the purpose of finding e.g. displacement from a v-t graph, you have to count areas below the x axis as negative.

 

[member 731016]

It should not refer to inflection points here. The first and second derivatives of v would need to exist and be continuous.

For the purpose of finding e.g. displacement from a v-t graph, you have to count areas below the x axis as negative.

Thank you for your reply @haruspex !

Why would the second derivative of v need to exist and be continuous?

Also I still don't understand how I calculated the displacement wrong since there is no negative velocities from t = 0 to t = 6 sec

Many thanks!

 

[haruspex]

Why would the second derivative of v need to exist and be continuous?

https://en.wikipedia.org/wiki/Inflection_point

there is no negative velocities from t = 0 to t = 6 sec

How true, but you fooled me with the last two terms in

$0.5 \times 3 \times 8 + 2 \times 8 + 1\times 4 + 1 \times 1 \times 4$.

If stopping at 6sec, where do those come from?

 

[member 731016]

https://en.wikipedia.org/wiki/Inflection_point

How true, but you fooled me with the last two terms in

If stopping at 6sec, where do those come from?

Thank you for your reply @haruspex!

Sorry I made a slight mistake with the last term. It should be

$0.5 \times 3 \times 8 + 2 \times 8 + 1\times 4 + 0.5 \times 1 \times 4 = 34 m$.

The last two terms $1\times 4 + 0.5 \times 1 \times 4 = 34 m$ are accounted for here on the graph in red and orange.

The solution seems to account for only the orange triangle ($1 \times 4$) giving $32 m$. However, I though displacement should the total area under the velocity curve over the interval $[0, 6] s$ so I included the red triangle to get $34 m$

Let me know what you think!

Many thanks!

 

[haruspex]

Thank you for your reply @haruspex!

Sorry I made a slight mistake with the last term. It should be

$0.5 \times 3 \times 8 + 2 \times 8 + 1\times 4 + 0.5 \times 1 \times 4 = 34 m$.

The last two terms $1\times 4 + 0.5 \times 1 \times 4 = 34 m$ are accounted for here on the graph in red and orange.
View attachment 322355
The solution seems to account for only the orange triangle ($1 \times 4$) giving $32 m$. However, I though displacement should the total area under the velocity curve over the interval $[0, 6] s$ so I included the red triangle to get $34 m$

Let me know what you think!

Many thanks!

Well, when you put it like that, I agree.
The book mistake is that they found the average speed between 5s and 7s, instead of between 5s and 6s.

 

[member 731016]

Well, when you put it like that, I agree.
The book mistake is that they found the average speed between 5s and 7s, instead of between 5s and 6s.

Interesting that makes a difference to their calculation! Thank you for your help @haruspex!

You mention average speed which makes me wonder why they could not have just used the average velocity over the entire interval from t = 0 to t = 6 sec :

$v_{avg} = \frac {v_i + v_f}{2} = \frac {x_f - x_i}{t}$
$\frac {0+ 4}{2} = \frac {x_f - 0}{6}$
$12m = x_f$

I now realize this because the average velocity formula $v_{avg} = \frac {v_i + v_f}{2}$ is only valid for constant acceleration. But the acceleration varies over the interval.

I'm not sure how to prove that the average velocity formula is only valid for constant acceleration thought.

Many thanks!

 

[haruspex]

how to prove that the average velocity formula is only valid for constant acceleration

You cannot prove it wrong in general because it might just happen to give the right answer sometimes. But to prove it is not a valid method you only have to construct one example where it gives the wrong answer.

 

[member 731016]

You cannot prove it wrong in general because it might just happen to give the right answer sometimes. But to prove it is not a valid method you only have to construct one example where it gives the wrong answer.

Thank very much for your help @haruspex !

 

[MatinSAR]

I'm not sure how to prove that the average velocity formula is only valid for constant acceleration thought.

You can prove that it is only right for constant acceleration.
For constant acceleration we have two main equations: (If we have $t_0=0$)
$x=x_0+v_{0}t+\frac 1 2 at^2$
$v=v_0+at$
Using $v=v_0+at$ we know that $a=\frac {v-v_0} {t}$. We put it in first equation then we have:
$x=x_0+v_{0}t+\frac 1 2 \frac {v-v_0} {t}t^2$
$x=x_0+v_{0}t+\frac 1 2 (v-v_0)t$
$x=x_0+v_{0}t+\frac 1 2 vt -\frac 1 2 v_{0}t$
$x-x_0=\frac 1 2 vt +\frac 1 2 v_{0}t$
$x-x_0=\frac 1 2 (v+v_0)t$
Compare it with $v_{avg}=\frac {x-x_0} {t}$→ $x-x_0=v_{avg}t$

You can see that $v_{avg}=\frac 1 2 (v+v_0)$

 

[member 731016]

You can prove that it is only right for constant acceleration.
For constant acceleration we have two main equations: (If we have $t_0=0$)
$x=x_0+v_{0}t+\frac 1 2 at^2$
$v=v_0+at$
Using $v=v_0+at$ we know that $a=\frac {v-v_0} {t}$. We put it in first equation then we have:
$x=x_0+v_{0}t+\frac 1 2 \frac {v-v_0} {t}t^2$
$x=x_0+v_{0}t+\frac 1 2 (v-v_0)t$
$x=x_0+v_{0}t+\frac 1 2 vt -\frac 1 2 v_{0}t$
$x-x_0=\frac 1 2 vt +\frac 1 2 v_{0}t$
$x-x_0=\frac 1 2 (v+v_0)t$
Compare it with $v_{avg}=\frac {x-x_0} {t}$→ $x-x_0=v_{avg}t$

You can see that $v_{avg}=\frac 1 2 (v+v_0)$

Thank you for your help @MatinSAR !