Poisson equation/zero padding and duplicating Green function

[fab13]

Hello,

I need to solve the Poisson equation in gravitational case (for galaxy dynamics) with Green's function by applying Fast Fourier Transform.

I don't understand the method used for an isolated system from (Hockney & Eastwood 1981); it says :

The convolution method described will solve a periodic system of sources with an arbitrary form of interaction. No conductors or boundaries are permitted in the system and, if these are present, the capacity matrix method must be used.

By an appropriate choice of Green's function the convolution method enables the potential to be found for an isolated source distribution. By isolated system, like a galaxy of stars, in which the only boundary condition is that the potential decays to zero correctly at infinity (i.e Φ∝r^-1).

The method, which we describe in the two dimensions, may be adapted to isolated systems if one is prepared to use only one-quarter of the available mesh points for the source distribution - say, the bottom left-hand corner, defined by 0≤p,q≤n/2. The source distribution over the remaining three-quarters of the system is made identically zero. Taking the interaction of point charges as an example, an interaction potential is constructed as follows :

$$G_{p,q}=(p^2+q^2)^{-1/2}\\ G_{n-p,q}}=G_{p,n-q}=G{n-p,n-q}=G_{p,q}\\ G_{0,0}=1\\ for 0≤p,q≤n/2 and p+q≠0$$

When this potential is repeated periodically, one sees that the correct r^-1 potential for a point charge at the origin is obtained within the region -n/2≤p,q≤n/2. At the boundary of this region there is a cusp, and outside the region the potential is incorrect. However, if we use only the bottom left-hand corner for the charge distribution and use only the potential in this region, the correct potential for an isolated system is obtained. The potential outside the bottom left-hand corner is incorrect, containing as it does not matter, since this potential is never used."

"The Fourier analysis being more straightforwardly performed in a periodic system, we use the "zero padding trick" for a N x N grid :

Let's consider the 2D case :

1. I compute the Green's function in real space, in the N x N grid

2. I duplicate and mirror the Green's function in the 3 "ghost" quadrants, so that the Green's function is now periodic in the Ng = 2N x 2N grid (see below figure)

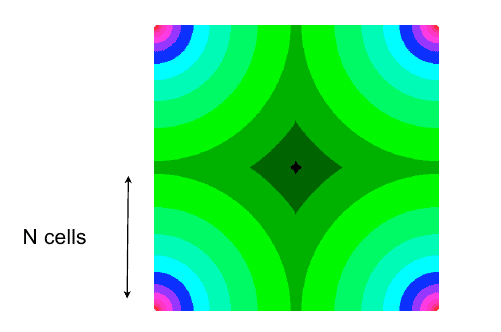
3. Set the density field to zero in the 3 ghosts quadrants. (see below figure)

4. Perform a forward FFT on the 2N x 2N grid : multiply the Fourier transform of Green's function by the Fourier transform of density field ( product which is equal to the Fourier transform of the gravitational potential)

5. Perform a backward FFT of the Fourier potential to get the potential in space.

I have 2 questions:

* Why we duplicate the Green function ? It seems like one wants to make it periodic but why ?

* Why do we "zero padding" on distribution charges ? Is it because the Green function is duplicated and stored on 2N points ?

Thanks in advance

 

[jvicens]

Hello,

Thank you for your questions. I will try to explain the method used in the forum post in more detail.

Firstly, let's start with the Poisson equation in gravitational case:

∇^2Φ = 4πGρ

where Φ is the gravitational potential, G is the gravitational constant, and ρ is the mass density.

The Green's function method is used to solve this equation by converting it into a convolution integral:

Φ(r) = ∫G(r-r')ρ(r')dr'

where G is the Green's function and r' is the position of the source mass.

Now, let's focus on the specific method described in the forum post. This method is used for an isolated system, meaning there are no boundaries or conductors present. In this case, the potential should decay to zero at infinity (Φ∝r^-1).

To use the convolution method for an isolated system, the Green's function needs to be adapted. This is because the Green's function for a periodic system, which is more straightforward to analyze using Fourier methods, does not decay to zero at infinity. Therefore, the Green's function needs to be modified to account for this boundary condition.

The method described in the forum post uses a "zero padding trick" to convert the problem into a periodic system. This is done by duplicating and mirroring the Green's function in the "ghost" quadrants, creating a periodic function in a 2N x 2N grid. This periodic function can then be analyzed using Fourier methods.

Now, to answer your questions:

1. Why do we duplicate the Green's function?

As mentioned before, the duplicated Green's function creates a periodic function that can be analyzed using Fourier methods. This is necessary because the original Green's function does not decay to zero at infinity, which is a requirement for an isolated system.

2. Why do we "zero padding" on distribution charges?

The "zero padding" is done to create a periodic density field. This is necessary because the Green's function has been duplicated and mirrored in the "ghost" quadrants, creating a larger grid of 2N x 2N points. The original density field only exists in the bottom left quadrant, so the other three quadrants are set to zero to match the size of the Green's function.

I hope this helps to clarify the method used for solving the Poisson equation in the gravitational case using Green