Poisson PDE in polar coordinates with FDM

[kicsicsibe]

I want to solve a Laplace PDE in a polar coordinate system with finite difference method.

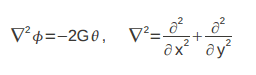
and the boundary conditions:

Here that I found in the internet:

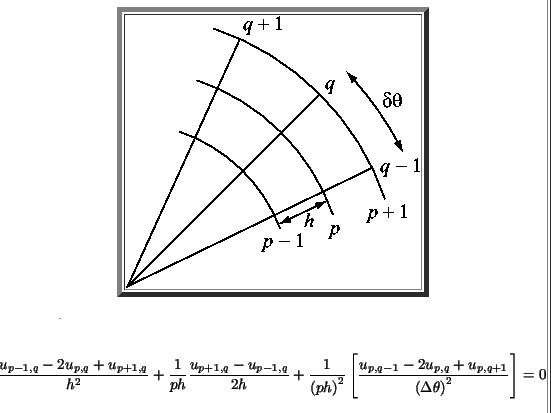
and the analytical result is:

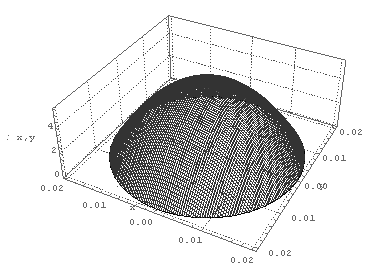
The question is how its works? Can I give an example or itd?Thanks

 

[jedishrfu]

If you're going to do this in polar coordinates then you need to use the Laplacian in polar coordinates

http://en.m.wikipedia.org/wiki/Laplacian

 

[kicsicsibe]

Thanks, I know this, but I search an example where this problem solved.