ashah99
- 55
- 2
- Homework Statement
- Please see below for homework statement
- Relevant Equations
- Please see below for useful equations
Hello all, sorry for the large wall of text but I'm really trying to understanding a problem from a study guide. I am quite unsure on how to approach the following multi-part problem. Any help would be appreciated.
Problem:

Useful references I'm using to attempt the problem


My attempt:
For part (a), my reasoning is the following, and if anyone can kindly check on these answers, that would be great.
(i) Poisson(5), since this describes the number of arrivals (hits) in a window, so the RV should be Poisson(lambda*T), where λ = 1 photon/us and T is 5 us duration, thus Poisson(5)
(ii) Poisson(2), Z is the number of events in [5,7], so this is Poisson(7-5) = Poisson(2)
(III) Exp(1), since waiting times of a Poisson process are i.i.d. Exponential with parameter λ = 1
(iv) Erlang(1,2) since this is the waiting time for the kth arrival
Based off the info above, then for parts (b) and (c) I get the following:
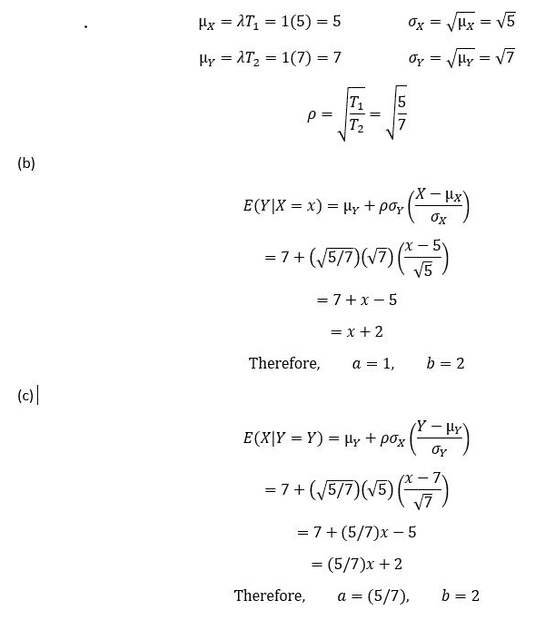
Problem:
Useful references I'm using to attempt the problem
My attempt:
For part (a), my reasoning is the following, and if anyone can kindly check on these answers, that would be great.
(i) Poisson(5), since this describes the number of arrivals (hits) in a window, so the RV should be Poisson(lambda*T), where λ = 1 photon/us and T is 5 us duration, thus Poisson(5)
(ii) Poisson(2), Z is the number of events in [5,7], so this is Poisson(7-5) = Poisson(2)
(III) Exp(1), since waiting times of a Poisson process are i.i.d. Exponential with parameter λ = 1
(iv) Erlang(1,2) since this is the waiting time for the kth arrival
Based off the info above, then for parts (b) and (c) I get the following: