- #1
Nikitin
- 735
- 27
This is polarization density.
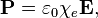 Can somebody explain to me why exactly this is so? My book just says that's how polarization is defined.. Can you guys give me an intuitive understanding of why? Only thing I know is that χ is related to κ, the dielectric constant, and κ is related to how well a dielectric polarizes.
Can somebody explain to me why exactly this is so? My book just says that's how polarization is defined.. Can you guys give me an intuitive understanding of why? Only thing I know is that χ is related to κ, the dielectric constant, and κ is related to how well a dielectric polarizes.
Last edited: