Polarization of Scattered Radiation, motivating definition?

[PhDeezNutz]

Homework Statement

First I'd like to say that this post is going to be a mixture of passages and derivations from two different books (Jackson and Zangwill)

According to Jackson and Zangwill (I've been primarily using Zangwill) the definition of Polarization of Scattered Radiation is

$\Pi \left(\theta \right) = \frac{\frac{d \sigma_\perp}{d \Omega} - \frac{d \sigma_\parallel}{d \Omega}}{\frac{d \sigma_\perp}{d \Omega} + \frac{d \sigma_\parallel}{d \Omega}} = \frac{\sin^2 \theta}{1 + \cos^2 \theta}$

I was able to reconcile the definitions/formulas for $\frac{d \sigma_\perp}{d \Omega}$ and $\frac{d \sigma_\parallel}{d \Omega}$ and of course I could just plug them into the formula given for $\Pi \left( \theta \right)$ and recover the formula above but I'm trying to understand it on a conceptual level. Which vectors are being projected onto which vectors?

(See picture below)

Relevant Equations

From Zangwill we have for polarized light

$\frac{d \sigma}{d \Omega} = r_e^2 \left(1 - \left|\hat{k} \cdot \hat{e}_0 \right|^2 \right)$

Where $r_e$ is the classical electron radius.

Figure from Jackson, the $0$ subscripts indicate incident waves whereas the lack of subscripts indicate the scattered wave.

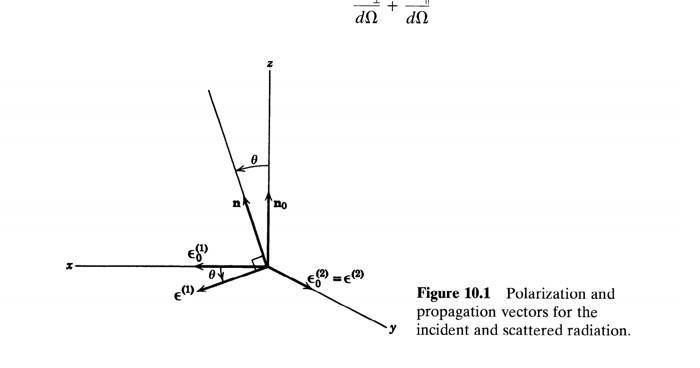
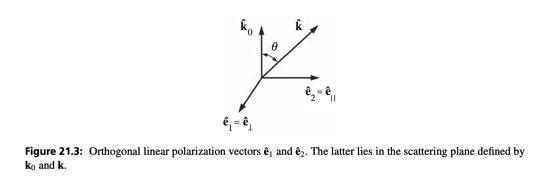
Figure from Zangwill, the hat $\hat{e}$ vectors are for the incident electric field. We are dealing with unpolarized light so we have two orthogonal polarization vectors. Likewise the $0$ subscript indicates the incident wave and the lack of subscripts indicate the scattered wave.

In order to find $\frac{d \sigma}{d \Omega}_{unpolarized}$ we merely take a statistical average of the$\frac{d \sigma}{d \Omega}$ for the two polarization vectors.

$\frac{d \sigma}{d \Omega}_{unpolarized} = \frac{1}{2} \left(\frac{d\sigma_{\perp}}{d \Omega} + \frac{d \sigma_{\parallel}}{d \Omega} \right) = \frac{\left( r_e^2 \right)}{2} \left[\left( 1 - \left| \hat{k} \cdot \hat{e}_{\perp} \right|^2\right) + \left( 1 - \left| \hat{k} \cdot \hat{e}_{\parallel} \right|^2 \right)\right] = \frac{1}{2} \left[ r_e^2 + r_e^2\left( 1 - \sin^2 \theta \right)\right] = \frac{r_e^2}{2} \left( 1 + \cos^2 \theta \right)$

So finding the differential cross sections for both the parallel and perpendicular incident E-field was easy enough but the next step is confusing. Carrying out the math is easy enough but reconciling the concept is difficult for me.

In Jackson's figure to find the numerator which vector do we want to project $\vec{\varepsilon_1}$ onto?

 

[TSny]

In Jackson's figure to find the numerator which vector do we want to project $\vec{\varepsilon_1}$ onto?

For scattering from a small dielectric sphere, Jackson derives $$\frac{d \sigma}{d \Omega} = k^4a^6 \left( \frac{\varepsilon_r - 1}{\varepsilon_r + 2} \right) \left|\vec \epsilon^{\,*} \cdot \vec \epsilon_0 \right|^2$$

Here, $\vec \epsilon$ corresponds to the polarization direction of the scattered wave and $\vec \epsilon_0$ corresponds to the polarization direction of the incoming wave. You need to decide what to choose for these vectors.

In general, $\vec \epsilon_0$ can point in any direction in the x-y plane of Jackson's figure. Thus, if $\vec \epsilon_0$ makes an angle $\phi$ to the x-axis, then $\vec \epsilon_0 = \cos \phi \, \vec \epsilon_0^{(1)} + \sin \phi \, \vec \epsilon_0^{(2)}$. For unpolarized incoming radiation, you will need to eventually average over all angles $\phi$.

For $\large \frac{d \sigma_{\perp}}{d \Omega}$, you want $\vec \epsilon$ to correspond to the scattered radiation being polarized perpendicular to the $\hat n$-$\hat n_0$ plane in Jackson's figure. So, choose $\vec \epsilon$ to be $\vec \epsilon^{(2)}$ in Jackson's figure. Then, $\left|\vec \epsilon^{\,*} \cdot \vec \epsilon_0 \right|^2 = \left|\vec \epsilon^{(2)} \cdot \vec \epsilon_0 \right|^2$

Note that $\hat n$ and $\hat n_0$ both lie in the x-z plane. Vectors $\vec \epsilon_0^{(1)}$ and $\vec \epsilon^{(1)}$ also lie in the x-z plane.

For $\large \frac{d \sigma_{\parallel}}{d \Omega}$, you want $\vec \epsilon$ to correspond to the scattered radiation being polarized parallel to the $\hat n$-$\hat n_0$ plane. So, what vector in Jackson's figure would you choose for $\vec \epsilon$ when finding $\large \frac{d \sigma_{\parallel}}{d \Omega}$ ?

 

[PhDeezNutz]

For dσ∥dΩdσ∥dΩ\large \frac{d \sigma_{\parallel}}{d \Omega}, you want ϵ⃗ ϵ→\vec \epsilon to correspond to the scattered radiation being polarized parallel to the n̂ n^\hat n-n̂ 0n^0\hat n_0 plane. So, what vector in Jackson's figure would you choose for ϵ⃗ ϵ→\vec \epsilon when finding dσ∥dΩdσ∥dΩ\large \frac{d \sigma_{\parallel}}{d \Omega} ?

We'd chose $\vec{\varepsilon}$ to be equal to $\vec{\varepsilon}_0^{(1)}$ if I followed your logic correctly. But to me that would mean the polarization is both the same before and after the scattering. How can that be?

 

[TSny]

We'd chose $\vec{\varepsilon}$ to be equal to $\vec{\varepsilon}_0^{(1)}$

No, the polarization of the scattered radiation must be perpendicular to $\hat n$.