Possible to calculate shear stress from this?

[EngChrisP]

Ok, so I would like to know if something is possible.

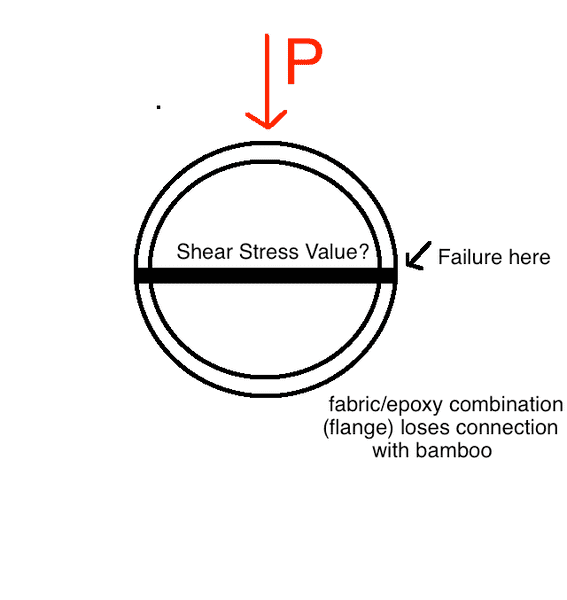
I have a bamboo ring, which has been cut in half, and had a piece of fabric soaked in epoxy placed in between to act as a flange.

Under compression, the main failure occurs at the fabric/bamboo connection, as a result of shear stress.

Is it possible to determine this shear stress value specific to the fabric and the bamboo from the applied load on top?

I have attached a diagram to try to explain things a bit better?

Many thanks for any help!

 

[Chestermiller]

Who says that the failure mechanism is shear stress?

 

[EngChrisP]

Who says that the failure mechanism is shear stress?

I've done a lot of tests and it does seem to be the case. Let's assume it is even though it might not be, how could that value be determined, if it actually can?

Thanks

 

[Chestermiller]

I've done a lot of tests and it does seem to be the case. Let's assume it is even though it might not be, how could that value be determined, if it actually can?

Thanks

You are dealing with a curved beam. Do you know how to analyze a curved beam problem?

 

[EngChrisP]

I do not, so I guess it is not possible to obtain shear stress from this problem? Thanks for the help anyway!

 

[Chestermiller]

I do not, so I guess it is not possible to obtain shear stress from this problem? Thanks for the help anyway!

It is possible, but you need to learn how to analyze loading and response of curved beams. Do you at least know how to analyze a straight beam?

 

[EngChrisP]

Oh ok, I do know how to analyze a straight beam yes.

 

[Chestermiller]

So now all you need to learn is how to extend this to cover curved beams.

 

[EngChrisP]

anyone willing to help supply an answer and not try to make themselves out to be smarter than someone else please? =)

 

[jrmichler]

Let me try. You state that you have a bachelor's degree and are working on a master's degree. I looked at two different undergrad mechanics of materials books, and both of them had a section on curved beams. At the master's degree level, you are expected to be able to read and learn material outside of what was covered in lecture. A quote from the forum rules: "Full solutions on a homework problem should never be given. Only hints and explanations are allowed."

We are trying to guide you through the process of solving this problem. We do this by helping you when you get stuck, or see you traveling down a mathematical dead end.

To answer your question in your first post: Yes, it is possible.

 

[EngChrisP]

Well I really don't know where to begin here to be honest!

 

[jrmichler]

Start with a free body diagram of the top curved piece. Give it your best shot, and we'll help you from there.

 

[Chestermiller]

Start with a free body diagram of the top curved piece. Give it your best shot, and we'll help you from there.

Or start by googling curved beams

 

[EngChrisP]

nvm guys i see what the vibe here is like, if no one wants to help me that's cool. Of course I've googled curved beams, I'm completely lost, and I don't see myself getting much help here. Thanks anyway guys.

 

[Chestermiller]

nvm guys i see what the vibe here is like, if no one wants to help me that's cool. Of course I've googled curved beams, I'm completely lost, and I don't see myself getting much help here. Thanks anyway guys.

Not so fast. We can still help you understand the development and application of the curved beam analysis. Please try to articulate for us the part of the development that you are having trouble with, and we will be glad to assist in getting you over the rough spots.