Potential difference of an electric circuit

[Guillem_dlc]

Homework Statement

Consider the circuit section of the figure. Determine the potential difference $V_a-V_b$.

Data: $\varepsilon_1=6\, \textrm{V}$; $\varepsilon_2=7\, \textrm{V}$; $R_1=2\, \textrm{k}\Omega$; $R_2=4\, \textrm{k}\Omega$.

Sol.: $11\, \textrm{V}$

Relevant Equations

Ohm's law

The figure is:

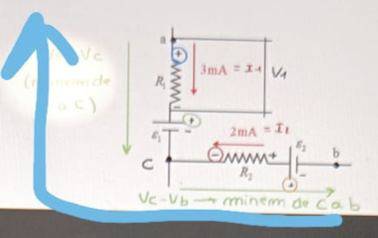
I have the solution to this problem:
We have two distinct branches
$$V_a-V_b=\overbrace{(V_a-V_c)}^{\textrm{INI}-\textrm{FIN}}+\overbrace{(V_c-V_b)}^{\textrm{FIN}-\textrm{INI}}$$
They have different intensities: $3\, \textrm{mA}$ and $2\, \textrm{mA}$
$V_A-V_C\rightarrow$ We have battery and resistor
$$V_A-V_C=+\overbrace{R_1I_1}^{V_1}+\varepsilon_1$$
$V_C-V_B\rightarrow$ High potential $\rightarrow V_B$
$$V_C-V_B=-\overbrace{R_2I_2}^{V_2}+\varepsilon_2$$The question that I have is: If they tell me the potential $V_a-V_b$ the green arrow it should not go the other way. Like the blue one I have drawn. So I would make $V_a-V_b=(V_c-V_b)+(V_a-V_c)$.

 

[kuruman]

The equation $V_a-V_b=(V_c-V_b)+(V_a-V_c)$ is always true if you add and subtract $V_a$ on the left side and is not saying anything new. My question to you is. "Are the 3 mA and 2 mA currents and their directions given to you by the problem?" If so, then you have charge accumulating somewhere between $a$ and $b$ unless the line I see extending down from C is a piece of wire carrying 1 mA down. Please clarify.

Also, please rephrase your question because I do not understand what you are really asking. Maybe my eyes are deceiving me but the arrow I see is blue, not green. Whatever its color, what is it supposed to indicate?

 

[Guillem_dlc]

Yes, the line of intensities is given by the statement.

The blue line is the route I think we should do, and the green line is the one the teacher put when solving the exercise.

 

[haruspex]

Yes, the line of intensities is given by the statement.

The blue line is the route I think we should do, and the green line is the one the teacher put when solving the exercise.

As far as I can make out, the question is the meaning of an arrow in a diagram between two potentials: should it point from the higher voltage to the lower (green) or the other way around (blue).
Higher to lower seems more natural to me, but it's just a convention; if there is no agreed standard, do whichever you like as long as you state it.

 

[haruspex]

you have charge accumulating somewhere between a and b

I read the diagram as being only part of a circuit. The unterminated lines above a, below c and to the right of b (and maybe some more in the upper right) go who knows where.

 

[Guillem_dlc]

As far as I can make out, the question is the meaning of an arrow in a diagram between two potentials: should it point from the higher voltage to the lower (green) or the other way around (blue).
Higher to lower seems more natural to me, but it's just a convention; if there is no agreed standard, do whichever you like as long as you state it.

Thanks! All understood!