Power generated by this current source

[Guillem_dlc]

Homework Statement

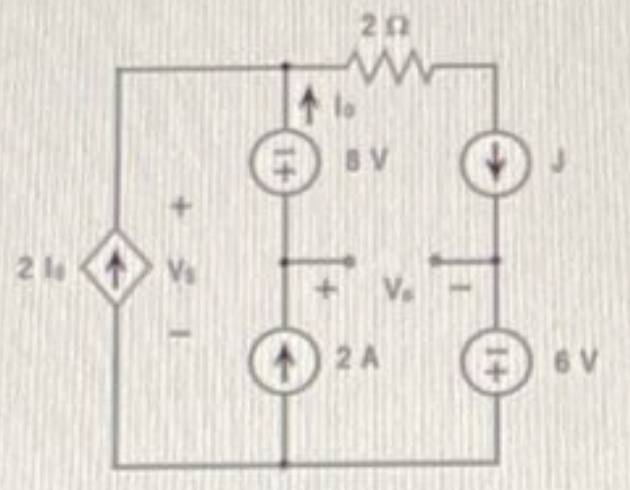
In the circuit of the figure knowing that $V_0=10\, \textrm{V}$ determine $V_S$ and the power generated by the source $J$.

Sol: $V_S=-4\, \textrm{V}$, $P_J=60\, \textrm{W}$

Relevant Equations

Kirchoff law

Figure:

My attempt at a solution:

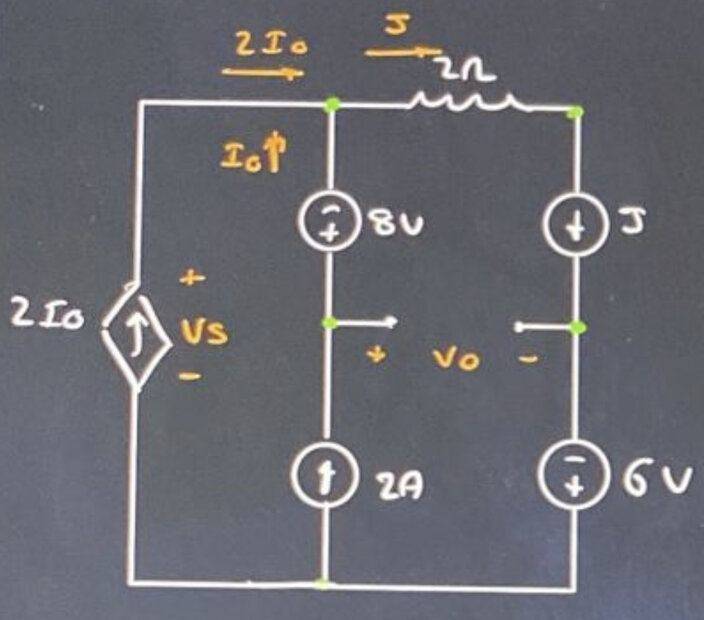
1st kirchoff law:
$$J=2I_0+I_0=6\, \textrm{A}$$

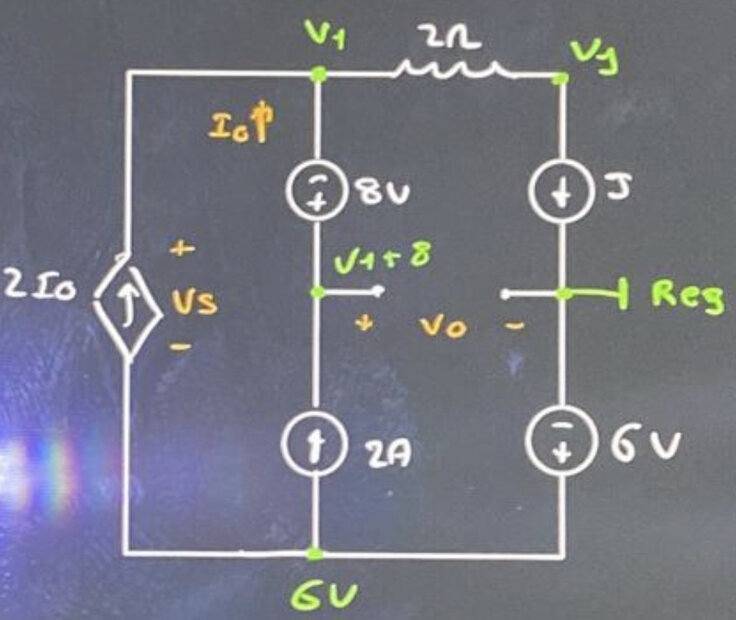
$$V_1+8=10\rightarrow \boxed{V_1=2}$$
$$V_1=6-V_S\rightarrow \boxed{V_S=-4\, \textrm{V}}$$
We are looking for $P$ generated in $J$
$$V_J=V_1-2\cdot J=2-2\cdot 6=-10\, \textrm{V}$$

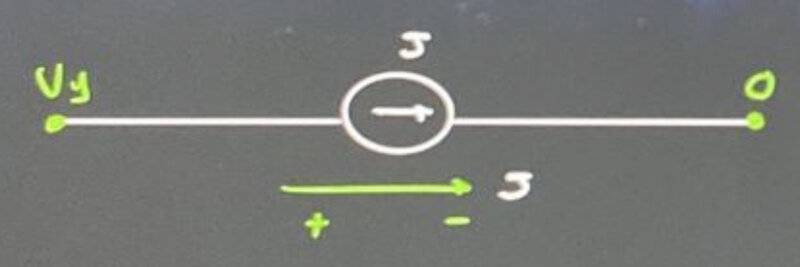
$$\boxed{P_{\textrm{gen}}=(V_J-0)J=-10\cdot 6=-60\, \textrm{W}}$$
Wouldn't this exercise do like this? I have tried it but the power is negative.

 

[haruspex]

Your $V_1=6-V_S$ should be $V_1=6+V_S$, but it looks like that was just a typo.
The rest looks right. I would not rule out the possibility that the answer is negative.

 

[Guillem_dlc]

Your $V_1=6-V_S$ should be $V_1=6+V_S$, but it looks like that was just a typo.
The rest looks right. I would not rule out the possibility that the answer is negative.

Is it negative?

 

[haruspex]

Is it negative?

As I wrote, your working looks fine, apart from that typo. So unless I am missing something the answer is negative.