Power of ten and math power notation

[KingGambit]

TL;DR Summary

Power of ten

Dear PF Forum,

I watched this video
10 ^ 10 ^ 10 ^ 5600

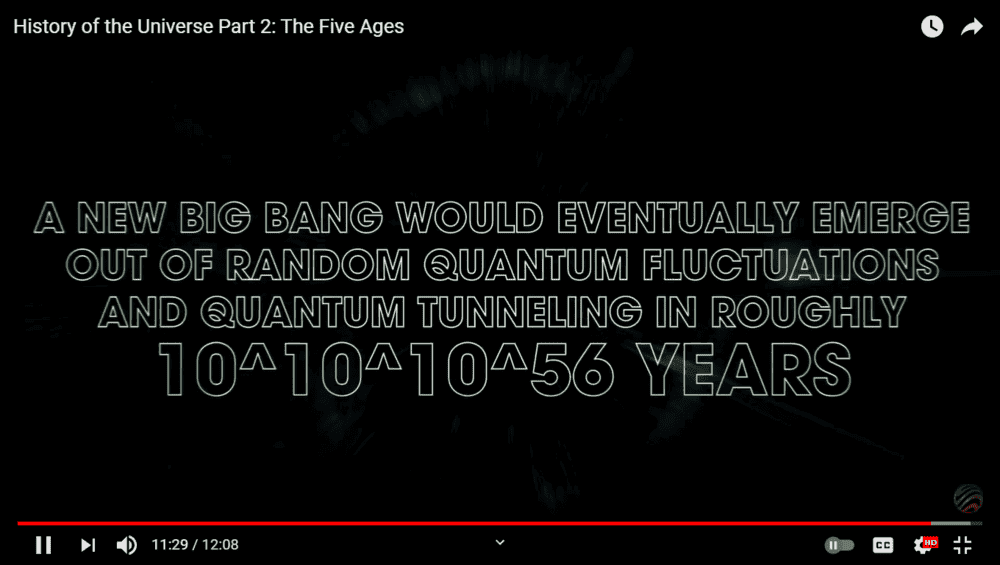
The narative says,
It is 1 followed by 5600 zeros

But that's not what I think,
I think it is 1 followed by I don't know.
What does this number means?

Is it
A: 10 ^ (10 ^ (10 ^ 56)))
or
B: ((10 ^ 10) ^ 10) ^ 56?

It says that
"As another possibility, during the dark era, the extreme low energy states might cause the localized quantum events to become major microscopic phenomena. At that point the smallest pertubation might lead to enormouse changes. In their paper spontaneus inflation and the origin of arrow of time, Sean Caroll and Jennifer Chan have calculated that the new Big Bang would eventually emerge out of random quantum fluctuations and quantum tunneling in roughly in ten to the power of ten to the power of ten to the power of 56 years.
That's one followed by 5600 zeros"

Well, is it 1 followed by 5600 zeros or (10 ^ (10 ^ 56))) zeros?
And judging from the physics involved, which one is true?

I mean 2 * (3 * (4 * 5 )) is the same as ((2 * 3) * 4) * 5 right. Or
2 + (3 + (4 + 5 )) = ((2 + 3) + 4) + 5 right.

And what about Penrose Number?
10¹⁰¹²³
Is it
A: 1 followed by 246 zeros
or
B: 1 followed by... you know.Here is the link:


Thank you very much for your help.

 

[mathman]

My guess is A $10^{10^{10^{5600}}}$

 

[jedishrfu]

Clearly, the narrator is not a numbers kind of guy.

 

[SSequence]

Is it
A: 10 ^ (10 ^ (10 ^ 56)))
or
B: ((10 ^ 10) ^ 10) ^ 56?

So when we write something like:
$\omega$^$\omega$^$\omega$^$\omega$
by default (if nothing else is mentioned) it usually is taken to mean:
$\omega$^($\omega$^($\omega$^$\omega$))=$\omega^{\omega^{\omega^{\omega}}}$
and not:
(($\omega$^$\omega$)^$\omega$)^$\omega$=$\omega^{\omega^3}$

One would guess that it should be similar for finite numbers too.

 

[jedishrfu]

It's taken to mean choice A.

As an example, if three is used instead of ten:

3^(3^3) = 3^27 = 7.62559748499e+12

-vs-

(3^3)^3 = 27^3 = 19683

 

[phinds]

Clearly, the narrator is not a numbers kind of guy.

I see you are practicing your use of understatement today

 

[KingGambit]

Summary:: Power of ten
And what about Penrose Number?
10¹⁰¹²³
Is it
A: 1 followed by 246 zeros
or
B: 1 followed by... you know.

I'm sorry.
Penrose number (10¹⁰¹²³) question should be
Is it
A: 1 followed by 246 1230 zeros
or
B: 1 followed by... you know.

I think there's a bug in my ALU or typo (if you call it a typo) in option A, but considering option B, my ALU just simply crashes.

 

[KingGambit]

So when we write something like:
$\omega$^$\omega$^$\omega$^$\omega$
by default (if nothing else is mentioned) it usually is taken to mean:
$\omega$^($\omega$^($\omega$^$\omega$))=$\omega^{\omega^{\omega^{\omega}}}$
and not:
(($\omega$^$\omega$)^$\omega$)^$\omega$=$\omega^{\omega^3}$

One would guess that it should be similar for finite numbers too.

Ow, thanks SSequence.