Practical design of an inverting Schmitt trigger with noise tolerance

[PhysicsTruth]

Homework Statement

Design an inverting Schmitt Trigger using the following specifications -
a) Threshold Voltage : 2V
b) Noise band tolerance allowed : +- 0.3V
c) Dual Power Supply = +-8V

Relevant Equations

a) $V_{out} = +-V_{sat}$
b) $V_{threshold} = \frac{R1}{R1+R2} V_{out}$

This is regarding the positive feedback of an Op-Amp and the inverting Schmitt trigger. This is a typical inverting Schmitt trigger -

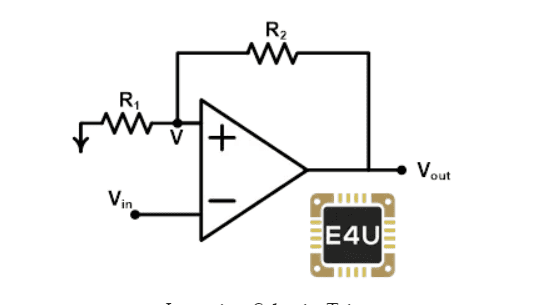
I need to design the Schmitt trigger such that I have a threshold voltage of around 2V, when my $+-V_{CC} = 8V$. The slew rate of the Op-Amp allows for a noise band as well, and the tolerance allowed is $+-0.3 V$, i.e. we can have the threshold voltage around 2.3V and 1.7V, to switch between $+V_{sat}$ and $-V_{sat}$, which should be almost equal to $+- V_{CC}$. In this way, I need to fix the biasing resistors. So, should I fix the resistors R1,R2 using the equation I've just provided above? Do I have to take into account the noise band tolerance in this as well?

 

[berkeman]

I would not count on Vsat being almost equal to the rail voltages. I would include Vsat in the equations instead of the rail voltages.

So yeah, write the equations to generate 2.3V and 1.7V trip points using the positive feedback resistors. Are you required to use the circuit exactly as you showed it, or can you use a couple other resistors to help you generate the 2V centerpoint of the hysteresis trip points?

You wrote:

 

[PhysicsTruth]

I would not count on Vsat being almost equal to the rail voltages. I would include Vsat in the equations instead of the rail voltages.

So yeah, write the equations to generate 2.3V and 1.7V trip points using the positive feedback resistors. Are you required to use the circuit exactly as you showed it, or can you use a couple other resistors to help you generate the 2V centerpoint of the hysteresis trip points?

You wrote:
View attachment 290628

Yeah, I'm allowed to use upto 3 resistors. Well, I've figured out a bit to set up a reference voltage to the ground from R1, to get the 2V centerpoint. But I'm not so sure of the equations. It would be helpful if you could give me certain hints for those , so that I can get going.

 

[PhysicsTruth]

I would not count on Vsat being almost equal to the rail voltages. I would include Vsat in the equations instead of the rail voltages.

So yeah, write the equations to generate 2.3V and 1.7V trip points using the positive feedback resistors. Are you required to use the circuit exactly as you showed it, or can you use a couple other resistors to help you generate the 2V centerpoint of the hysteresis trip points?

You wrote:
View attachment 290628

Also, the rail voltages differ from the saturation voltages by about 0.2V for the 741 IC open loop comparator. I've checked it on my oscilloscope.

 

[berkeman]

Also, the rail voltages differ from the saturation voltages by about 0.2V for the 741 IC open loop comparator. I've checked it on my oscilloscope.

Exactly, so a significant fraction of the 0.6V hysteresis window...

 

[berkeman]

Yeah, I'm allowed to use upto 3 resistors. Well, I've figured out a bit to set up a reference voltage to the ground from R1, to get the 2V centerpoint.

So redraw the circuit with the split resistors that feed into the + input, and then figure out what ratios you need to get the +/- 0.3V hysteresis...

 

[PhysicsTruth]

So redraw the circuit with the split resistors that feed into the + input, and then figure out what ratios you need to get the +/- 0.3V hysteresis...

Yeah, I'm trying.

 

[PhysicsTruth]

So redraw the circuit with the split resistors that feed into the + input, and then figure out what ratios you need to get the +/- 0.3V hysteresis...

But, the problem is that, I've only a dual power supply, to provide the rail voltages. So, I need to figure out how to use a third resistor to set up that 2V reference.

 

[berkeman]

But, the problem is that, I've only a dual power supply, to provide the rail voltages. So, I need to figure out how to use a third resistor to set up that 2V reference.

Try this to start -- Draw 2 resistors that are connected vertically in series, with the top end connected to V+ and the bottom end tied to V-. Tie the mid-point of those resistors to the + input of the opamp, and leave your positive feedback resistor tied to the + input as well. Maybe start with the two vertical resistors having values around 10kOhm, but tune that to make the center point be 2.0V instead of 0.0V.

Then calculate what the value of the positive feedback resistor has to be to offset that + input to the opamp by +/-0.3V (approximately) when the output of the opamp saturates at +/-Vsat. Then calculate what the actual voltage numbers are at the + input (they will be slightly different from your desired 2.3V and 1.7V). Why is that? Is the error acceptable?

 

[PhysicsTruth]

Try this to start -- Draw 2 resistors that are connected vertically in series, with the top end connected to V+ and the bottom end tied to V-. Tie the mid-point of those resistors to the + input of the opamp, and leave your positive feedback resistor tied to the + input as well. Maybe start with the two vertical resistors having values around 10kOhm, but tune that to make the center point be 2.0V instead of 0.0V.

Then calculate what the value of the positive feedback resistor has to be to offset that + input to the opamp by +/-0.3V (approximately) when the output of the opamp saturates at +/-Vsat. Then calculate what the actual voltage numbers are at the + input (they will be slightly different from your desired 2.3V and 1.7V). Why is that? Is the error acceptable?

I've been trying this circuit out for some time now, but I don't know why am I not being able to come up with equations to formulate the ratio of resistors and so on. Probably I'm panicking a bit with the design specifications.

 

[berkeman]

Well, just start thinking in tems of what the feedback resistor $R_f$ needs to be to offset the input voltage divider voltage. Conceptually you should see that you will find that $R_f > R_i$ to offset the + input voltage by a small percentage of the supply voltages...

Can you show us the equations you are writing so far tor calculating $R_f$ when given the vertical voltage divider with about 2x 10kOhm resistors? Maybe try doing it first assuming a 0.0V switching centerpoint instead of the slightly offset 2.0V...

 

[PhysicsTruth]

Well, just start thinking in tems of what the feedback resistor $R_f$ needs to be to offset the input voltage divider voltage. Conceptually you should see that you will find that $R_f > R_i$ to offset the + input voltage by a small percentage of the supply voltages...

Can you show us the equations you are writing so far tor calculating $R_f$ when given the vertical voltage divider with about 2x 10kOhm resistors? Maybe try doing it first assuming a 0.0V switching centerpoint instead of the slightly offset 2.0V...

Fine. But another thing I've been noticing is that the peak-to-peak input voltage provided by my function generator decreases, as I try to tinker around with the resistors.

 

[PhysicsTruth]

Well, just start thinking in tems of what the feedback resistor $R_f$ needs to be to offset the input voltage divider voltage. Conceptually you should see that you will find that $R_f > R_i$ to offset the + input voltage by a small percentage of the supply voltages...

Can you show us the equations you are writing so far tor calculating $R_f$ when given the vertical voltage divider with about 2x 10kOhm resistors? Maybe try doing it first assuming a 0.0V switching centerpoint instead of the slightly offset 2.0V...

Here are the equations which I've finally come up with -

Let the voltage be $+V_{CC}$. Now, writing the KCL equation, we have -

$\frac{V_{CC} - V_{+}}{R1} - \frac{V_{+}}{R2} - \frac{V_{out} - V_{+}}{Rf} = 0$

where R2 is the resistor to the ground, Rf is the feedback resistor, and R1 is connected to $+V_{CC}$.

Finally, we get $V_{+} = (\frac{1}{Rf+R1+R2})(\frac{V_{CC}}{R1} + \frac{V_{out}}{Rf})$

Now, the tripping voltages would be +2.3V and +1.7V. So, for the upper tripping point, $+V_{sat}$ is to be used, which is the high state, and for the lower point, $-V_{sat}$, which is the low state. Am I correct in these? Can I move on to determine the resistor ratio from here, or do I need to deduce more?

 

[PhysicsTruth]

Here are the equations which I've finally come up with -

Let the voltage be $+V_{CC}$. Now, writing the KCL equation, we have -

$\frac{V_{CC} - V_{+}}{R1} - \frac{V_{+}}{R2} - \frac{V_{out} - V_{+}}{Rf} = 0$

where R2 is the resistor to the ground, Rf is the feedback resistor, and R1 is connected to $+V_{CC}$.

Finally, we get $V_{+} = (\frac{1}{Rf+R1+R2})(V_{CC} + V_{out})$.

Now, the tripping voltages would be +2.3V and +1.7V. So, for the upper tripping point, $+V_{sat}$ is to be used, which is the high state, and for the lower point, $-V_{sat}$, which is the low state. Am I correct in these? Can I move on to determine the resistor ratio from here, or do I need to deduce more?

Something like this, I guess.

 

[berkeman]

Here are the equations which I've finally come up with -

Let the voltage be $+V_{CC}$. Now, writing the KCL equation, we have -

$\frac{V_{CC} - V_{+}}{R1} - \frac{V_{+}}{R2} - \frac{V_{out} - V_{+}}{Rf} = 0$

where R2 is the resistor to the ground, Rf is the feedback resistor, and R1 is connected to $+V_{CC}$.

Finally, we get $V_{+} = (\frac{1}{Rf+R1+R2})(V_{CC} + V_{out})$.

Now, the tripping voltages would be +2.3V and +1.7V. So, for the upper tripping point, $+V_{sat}$ is to be used, which is the high state, and for the lower point, $-V_{sat}$, which is the low state. Am I correct in these? Can I move on to determine the resistor ratio from here, or do I need to deduce more?

The last equation can't be correct, since the dimensions of the LHS and RHS don't match.

Yuo can write two equations, one for when Vout is high at +Vsat and one for when Vout is low at -Vsat. You can call R1 a known, and use the two equations to solve for the other two resistors.

I would also do it both for the configuration you show (with R2 to ground) and for the configuration that I originally suggest with R2's bottom end connected to the V- power rail. You may get better accuracy with one or the other configuration, but I'm not sure.

 

[PhysicsTruth]

The last equation can't be correct, since the dimensions of the LHS and RHS don't match.

Yuo can write two equations, one for when Vout is high at +Vsat and one for when Vout is low at -Vsat. You can call R1 a known, and use the two equations to solve for the other two resistors.

I would also do it both for the configuration you show (with R2 to ground) and for the configuration that I originally suggest with R2's bottom end connected to the V- power rail. You may get better accuracy with one or the other configuration, but I'm not sure.

Yeah, I missed the resistors R1 and Rf, I've modified.

 

[PhysicsTruth]

The last equation can't be correct, since the dimensions of the LHS and RHS don't match.

Yuo can write two equations, one for when Vout is high at +Vsat and one for when Vout is low at -Vsat. You can call R1 a known, and use the two equations to solve for the other two resistors.

I would also do it both for the configuration you show (with R2 to ground) and for the configuration that I originally suggest with R2's bottom end connected to the V- power rail. You may get better accuracy with one or the other configuration, but I'm not sure.

Can you tell me one thing though, how do I know that the reference is now set to 2V, and not 0V? How to determine this?

 

[berkeman]

Can you tell me one thing though, how do I know that the reference is now set to 2V, and not 0V? How to determine this?

The voltage divider of R1 and R2 (and the voltages at each end of that 2-resistor string) determine the mid-point voltage at the + input to the opamp (with Rf not connected yet). Connecting Rf offsets the + input voltage higher or lower, depending on the value of Vout and the ratio of Rf to R1 and R2.

 

[PhysicsTruth]

Thanks a lot for guiding me through this! I've finally found the ideal ratios by plotting the graphs and run the simulations as well.

 

[berkeman]

Great! Can you share what you found? Did you test this using both ground and V- as the low end of the voltage divider to see if there was any difference in accuracy or other considerations? I'd actually be interested in seeing that.

 

[PhysicsTruth]

Great! Can you share what you found? Did you test this using both ground and V- as the low end of the voltage divider to see if there was any difference in accuracy or other considerations? I'd actually be interested in seeing that.

Sure. I plotted R1 against Rf and obtained something like this -

So, I set the value of R1, and found Rf from that, and went on to find R2. The output does work really well. But, at first I had thought that the output was not in sync with the saturation voltage of the Op-Amp, and then I went on to check that due to loose connections, I had made a mistake, the saturation voltages actually differed from the rail voltages by about 0.9V! This quite explains the output as well!

 

[PhysicsTruth]

Great! Can you share what you found? Did you test this using both ground and V- as the low end of the voltage divider to see if there was any difference in accuracy or other considerations? I'd actually be interested in seeing that.

I haven't yet tested the other configurations as well, as I've something more to do with the Schmitt trigger. Once I'm done, I'm intrigued enough to try out the other configurations for accuracy comparisons.