Precession of a gyroscope in freefall

[ago01]

Imagine I have the following gyroscope:

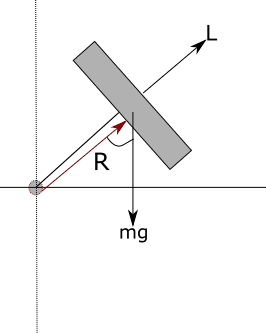
This gyroscope has been spun up with significant angular momentum and rests on a platform below it. It's offset at an angle and so I've drawn the R vector from the axis of rotation.

So the only force being applied right now is gravitational force $mg$. It's from this force that we get the gyroscope precessing.

But let's say I take the gyroscope on top of a ladder and drop it. The gyroscope stops precessing during the fall! Now I am trying to explain this. The professor stated that the reason is because "$mg$ goes to zero in free fall". In normal linear forces this made sense to me because if we are in free fall there is no normal force pushing up, so our apparent weight is zero. However we still have weight $mg$.

But in this case we are now talking about the gyroscope. When I drop the gyroscope it is experiencing only gravitational force pulling it down towards earth. The platform below it is not "stuck" to the ground, so it's falling at the same rate as the gyroscope. In the gryoscope-platform system the normal force and gravitational force cancel. Looking at it externally however, how is $mg$ going to zero here? It is still experiencing a gravitational force downward, and so should be experiencing the same torque it would feel sitting safe on the ground since it's being pulled down to Earth with that force - even though the platform is not "pushing back" on it due to freefall. But this is not true! I've seen it with my own eyes!

Can anyone help me explain this? Of course we'll assume air drag is negligible.

 

[italicus]

So the only force being applied right now is gravitational force mg. It's from this force that we get the gyroscope precessing.

Hi
This is Not correct.
When the Lower extremity of the axis is supported by a plane, fixed in an inertial reference frame, the upward reaction of the plane (a vector of course) has the same value of mg. The two forces form a couple, which gives the torque that causes variation of the angular momentum, that is precession.
When the gyroscope is in free fall, onlly P=mg acts, according to an inertial esternal obs, there is no couple, and no torque: the rotation axis falls remaining parallel to itself, only the first cardinal equation of rigid body dynamics apply.
What if the gyroscope is in a r. f. in free fall, for example a lift, and you are inside? The reference frame now isn’t inertial, an apparent force acts on all objects , for the gyroscope it is F = -ma = - mg, vectorially opposed to P= mg. So in the r.f. of the lift the resultant force is zero.
As you can see, two different points of view take to the same result, of course.

 

[ago01]

When the Lower extremity of the axis is supported by a plane, fixed in an inertial reference frame, the upward reaction of the plane (a vector of course) has the same value of mg. The two forces form a couple, which gives the torque that causes variation of the angular momentum, that is precession.

I see so the normal force is acting on the point it's balancing on. I'm having trouble imagining how the vector works out as it would be directly up the axis of rotation (off the contact point on the ground). Now that you mention it, it makes sense this would torque the gyroscope since the normal force is not pushing straight up (similar to on an incline) and so it causes it to experience torque and precess.

When the gyroscope is in free fall, onlly P=mg acts, according to an inertial esternal obs, there is no couple, and no torque: the rotation axis falls remaining parallel to itself, only the first cardinal equation of rigid body dynamics apply.

So naturally because even though I dropped it still "attached" to the platform, the platform and the gyro are both falling and so there's no reaction force being applied. Since there's no reaction force, there's no torque (since this is one part of the way the torque is generated) and it simply falls parallel to the axis of rotation (the direction of $mg$). Is this correct?

 

[DaveE]

it still "attached" to the platform, the platform and the gyro are both falling and so there's no reaction force being applied. Since there's no reaction force, there's no torque (since this is one part of the way the torque is generated) and it simply falls parallel to the axis of rotation (the direction of mg). Is this correct?

Yes.
The force $mg$, or the acceleration $g$, is applied equally to everything in your diagram (including the platform) during free fall. In the gyro frame of reference, this is the same as no force applied.

 

[italicus]

To be more precise and add some more considerations, the axis must be prevented from slipping on the plane (inertial rf). Therefore, a sufficient friction force is to be exerted by the plane, in order to compensate the push of the axis to the left ( refer to you drawing). So the total reaction of the plane is not only normal, but has a horizontal component as well. This one doesn’t have no effect on precession , because it only equilibrates the push of the axis. Clear?

 

[wrobel]

The Euler top (free rigid body) can precess as well

 

[italicus]

Yes of course; but the OP request concerned a heavy top in the gravitational Earth field, with the lower axis end touching a platform. For a short period of time, a “local “reference frame solidal to Earth can be considered inertial, but then you have always to take into account the gravitational field, that can be considered vectorially constant for the same period, and a small space extension(this means local).
A different situation is that of the r.f. In free fall…

 

[vanhees71]

Hi
This is Not correct.
When the Lower extremity of the axis is supported by a plane, fixed in an inertial reference frame, the upward reaction of the plane (a vector of course) has the same value of mg. The two forces form a couple, which gives the torque that causes variation of the angular momentum, that is precession.
When the gyroscope is in free fall, onlly P=mg acts, according to an inertial esternal obs, there is no couple, and no torque: the rotation axis falls remaining parallel to itself, only the first cardinal equation of rigid body dynamics apply.
What if the gyroscope is in a r. f. in free fall, for example a lift, and you are inside? The reference frame now isn’t inertial, an apparent force acts on all objects , for the gyroscope it is F = -ma = - mg, vectorially opposed to P= mg. So in the r.f. of the lift the resultant force is zero.
As you can see, two different points of view take to the same result, of course.

In other words: the gyroscope in free fall in the homogeneous gravitational field of the Earth behaves (from the point of view of the free-falling observer) as a free top (as it should due to the equivalence principle!).

 

[ago01]

To be more precise and add some more considerations, the axis must be prevented from slipping on the plane (inertial rf). Therefore, a sufficient friction force is to be exerted by the plane, in order to compensate the push of the axis to the left ( refer to you drawing). So the total reaction of the plane is not only normal, but has a horizontal component as well. This one doesn’t have no effect on precession , because it only equilibrates the push of the axis. Clear?

Not quite clear yet. Is this for the stationary or dropping gyroscope? I'm having trouble imaging a pushing to the left due to friction. I've never actually spun a gryoscope on something like ice (now I am going to have to try it!) but it seems like if the surface was frictionless the gyro would simply fall over because it would want to precess counter-clockwise, but since the contact point can't "stick" (due to friction) it slips and falls over.

So this makes sense. I think you're referring to why the gyro on the platform stands up when on the ground. There's a horizontal component similar to what we see in an incline plane. So, this opposes friction and those forces balance, allowing the gyroscope to precess about it's axis of rotation.

 

[italicus]

. Is this for the stationary or dropping gyroscope?

This is for the”stationary “ gyroscope of your drawing, which could slip toward the left if not prevented to do, by friction or a small step , say.
The gyroscope in free fall…falls freely!

Forgive me for my poor English, physics uses the universal language of math.
I guess you’ve understood what I am saying.

 

[italicus]

So this makes sense. I think you're referring to why the gyro on the platform stands up when on the ground. There's a horizontal component similar to what we see in an incline plane. So, this opposes friction and those forces balance, allowing the gyroscope to precess about it's axis of rotation.

I am not sure I have understood. The gyro stands up initially with its axis in vertical (even not perfectly…) resting on the platform and held by you; and is given an angular momentum L = I\omega. Were the plane perfectly smooth, it would remain spinning in that position for ever. But “perfect smoothness “ is an abstraction, sooner or later the axis receives impulses by the rough surface, and the gyro starts to incline: at this moment, the torque due to P and N gives strart to the precession , as already told,