- #1
kurt101
- 284
- 35
I have previously posted Preserving local realism in the EPR experiment
.
I have since given up on simulating local realism since I now understand it is impossible. However I have not given up on causality. Attached is code that simulates the EPR experiment and gives the same result as what quantum mechanics predicts.
The algorithm is simple and inspired by the quantum eraser experiment Quantum_eraser_experiment
In other words, I could only understand the result of the quantum eraser experiment by rationalizing it with the following algorithm:
The first entangled photon interacts with its polarizer and immediately gives the other entangled photon the result of its interaction. Other than this, the entangled photons interact normally with their respective polarizers.
This algorithm preserves causality when simulating the EPR and quantum eraser experiments and perhaps it would be correct to say it also preserves local reality since the mechanism is instant or FTL. Or am I twisting definitions here?
Here is the code that simulates this.
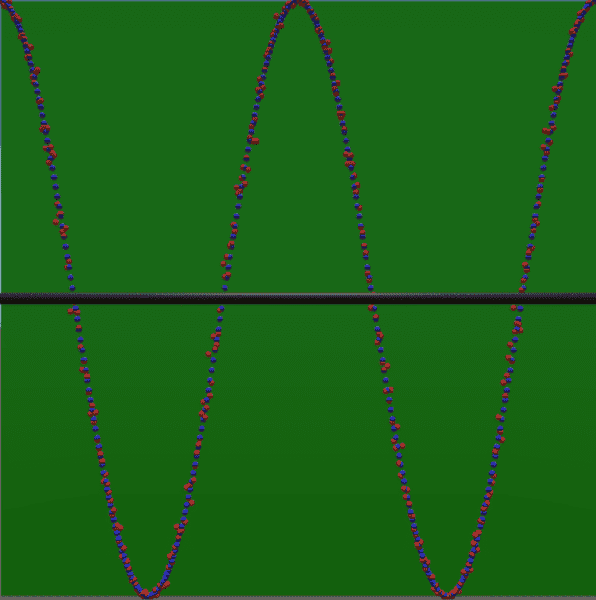
The result of the simulation gives the same result as quantum mechanics regardless of what angles I use for the respective polarizers. The blue spheres represent the quantum mechanics prediction and the red spheres represent the result of the simulation.
I assume that this type of mechanism has been explored by others. What are the problems with it?
Is entanglement considered a special case or is entanglement a part of any particle interaction?
If entanglement is involved in all particle interactions, could it explain why the probability amplitudes in quantum mechanics are complex functions that require the complex conjugates to resolve the probability?
Thanks for answers. I hope my questions are not too speculative in nature to get moderated. I certainly think some level of speculative questions can help in understanding science.
.
I have since given up on simulating local realism since I now understand it is impossible. However I have not given up on causality. Attached is code that simulates the EPR experiment and gives the same result as what quantum mechanics predicts.
The algorithm is simple and inspired by the quantum eraser experiment Quantum_eraser_experiment
In other words, I could only understand the result of the quantum eraser experiment by rationalizing it with the following algorithm:
The first entangled photon interacts with its polarizer and immediately gives the other entangled photon the result of its interaction. Other than this, the entangled photons interact normally with their respective polarizers.
This algorithm preserves causality when simulating the EPR and quantum eraser experiments and perhaps it would be correct to say it also preserves local reality since the mechanism is instant or FTL. Or am I twisting definitions here?
Here is the code that simulates this.
Code:
// Return the result of a particle interacting with a polarizer and then the detector. The result is either true or false.
// The iteraction also results in the particleAngle taking on the value of the polarizerAngle
// and the particleVector being rotated.
bool InteractWithPolarizer(float polarizerAngle, ref float particleAngle, ref Vector3 particleVector)
{
Quaternion rotation;
float angleDifference;
float dotProduct;
float rotationAngle;
bool result = false;
// Determine how much to rotate the particleVector
angleDifference = particleAngle - polarizerAngle;
particleAngle = polarizerAngle;
rotationAngle = Mathf.Pow(Mathf.Sin(angleDifference * Mathf.Deg2Rad), 2f) * Mathf.PI / 2f * Mathf.Rad2Deg;
rotation = Quaternion.AngleAxis(rotationAngle, leftParticle.direction); // angle is in degrees
particleVector = rotation * particleVector;
particleVector.Normalize();
// Compare with detector to determine if final state is up or down
// (the angle of the detector vector does not matter)
dotProduct = Vector3.Dot(particleVector, Vector3.up);
if ((dotProduct * dotProduct) > 0.5f)
{
result = true;
}
return result;
}
// One particle uses the result of the other particle as a result of entanglement.
void RunMethod45(out bool leftUp, out bool rightUp)
{
// Properties of the entangled particle
float particleAngle = this.GetRandom(-180f, 180f);
Vector3 particleVector = this.GetRandomVector(true);
// Determine left particle
leftUp = this.InteractWithPolarizer(leftPolarizer.angle, ref particleAngle, ref particleVector);
// Determine right particle
// Right particle inherits the properties of the left entangled particle after it interacted with its polarizer
// because the left entangled particle interacted with its polarizer first (the order does not matter)
rightUp = this.InteractWithPolarizer(rightPolarizer.angle, ref particleAngle, ref particleVector);
}The result of the simulation gives the same result as quantum mechanics regardless of what angles I use for the respective polarizers. The blue spheres represent the quantum mechanics prediction and the red spheres represent the result of the simulation.
I assume that this type of mechanism has been explored by others. What are the problems with it?
Is entanglement considered a special case or is entanglement a part of any particle interaction?
If entanglement is involved in all particle interactions, could it explain why the probability amplitudes in quantum mechanics are complex functions that require the complex conjugates to resolve the probability?
Thanks for answers. I hope my questions are not too speculative in nature to get moderated. I certainly think some level of speculative questions can help in understanding science.
