Pressure delta 1.0 bar: 0.0 to 1.0 vs 1.0 to 2.0

[kaare_t]

TL;DR

Approaching absolute vacuum versus not absolute vacuum with the same delta P, forces involved

Hi,

New member here. I have no higher education, please excuse me if I'm asking an obvious question, and feel free to reply with more questions if my post is unclear! And please feel free to correct me if I'm using wrong term(s), or wrong assumptions.

My question is related to pressure, and more specifically if approaching an absolute vaccum (I know it's impossible to reach 0.0 bar, but my post is more of a thought-experiment).

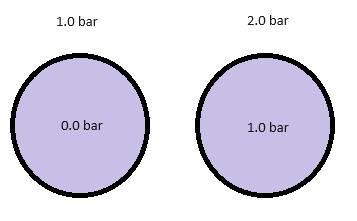
My question is if there is any difference between two configurations where the delta pressure is 1.0 bar in both configurations (see picture). The picture is of two different cylinders that are closed, and in both examples my intention is to have a delta P of 1.0 bar. Are there any other forces than the delta pressure involved in such an example, or can I assume that the only force applied is the delta P?

My own wonderings are about approaching 0.0 bar, will the forces acting on the pipe-wall look similar to e.g. an object approaching the speed of light (a curve of applied energy that exponentially grows into infinity)? And if so, can I assume that pressure is related to energy in a sense that you would need infinite energy to create an absolute vacuum?

 

[Lnewqban]

Welcome!

Normally, differential pressure is what matters.
Not if the machine doing the work has dissimilar conditions.
Are you familiar with the concepts of absolute and relative pressures?
The main problem with reaching deep vacuum is not energy used, but to catch the increasingly scarce molecules of the gas inside the container.

 

[kaare_t]

Hi, and many thanks!

I realize I'm asking two questions at the same time, I hope that's OK. I'm also interested in a bit more detailed answers, so I'm trying to be more precise below.

Normally, differential pressure is what matters.
Not if the machine doing the work has dissimilar conditions.

I'm not sure what you mean by

1. Normally, ......
2. ....... dissimilar conditions

in my scenario, would you please specify a bit more?

Most importantly, are the forces acting on the pipe-wall the same, as long as the differential pressure is 1.0 bar, regardless of inner/outer absolute pressure? Mathematically I think the test-parameters would look like:

Inner absolute pressure = x, Outer absolute pressure = x+1​

X can be any number​

The forces acting on the pipe-wall will always be the same?​

The main problem with reaching deep vacuum is not energy used, but to catch the increasingly scarce molecules of the gas inside the container.

Thanks. But the process of creating a vacuum requires energy, and to my understanding reaching 0.0 bar is not possible just like reaching 0.0 Kelvin is not possible. I made an assumption that both of these might be in the same category as reaching the speed of light. To my understanding

can be translated to accelleration requires energy, but it requires an infinite amount of energy to reach the speed of light for any object with a mass. Hence the exponential graph.

To try and visualize, if we had graphs of consumed energy for theoretically reaching:

1. c (speed of light)
2. 0.0 Kelvin
3. 0.0 bar

Would they basically look the same way (discarding the axis-values of speed, temperature and pressure)?

If energy is not the correct factor to describe the process of creating vacuum, would you please provide me the correct factor that limits the ability to create 0.0 bar?

Thanks for any help and pointers!

 

[Chestermiller]

Hi, and many thanks!

I realize I'm asking two questions at the same time, I hope that's OK. I'm also interested in a bit more detailed answers, so I'm trying to be more precise below.I'm not sure what you mean by

1. Normally, ......
2. ....... dissimilar conditions

in my scenario, would you please specify a bit more?

Most importantly, are the forces acting on the pipe-wall the same, as long as the differential pressure is 1.0 bar, regardless of inner/outer absolute pressure? Mathematically I think the test-parameters would look like:

Inner absolute pressure = x, Outer absolute pressure = x+1​

X can be any number​

The forces acting on the pipe-wall will always be the same?T​

The net radial are the same in both cases, but the individual forces on the pipe surfaces are not the same. And the hoop forces within the pipe walls are the same. This is provided that the wall material is incompressible and the wall thicknesses are small compared to the radii. If not,, the internal stresses and strains within the walls will differ in the two cases

 

[Hill]

to my understanding reaching 0.0 bar is not possible

There is on average one atom per cubic centimeter in the interstellar space of the Milky Way. So, one could isolate a volume of this space with no atoms in it. Wouldn't it make 0.0 bar?

 

[berkeman]

So, one could isolate a volume of this space with no atoms in it.

How would you clean out the inside of the container first?

 

[Hill]

How would you clean out the inside of the container first?

I'd assemble the container in space.

 

[kaare_t]

Thanks for all inputs, I'm following up again with some additional wonderings.

This is provided that the wall material is incompressible and the wall thicknesses are small compared to the radii. If not,, the internal stresses and strains within the walls will differ in the two cases

Does it mean that the delta pressure forces are always acting on the pipe-walls in the same way (as stated in the first reply to my post), but in the absence of pressure the material of the walls facing lach of pressure will suffer "more" from it's internal stresses in it's chemical bonds? Or in a different sentence; without external pressure, materials are "forced less together"?

If I understood the above correctly, it kind of answers both my questions I think. Does there exist any graphs or similar that shows these effects? And does there exist some kind of issue if we raised the pressure super-high (but still with a delta P of 1.0 bar)?

Wouldn't it make 0.0 bar?

Are you asking, or stating? I agree, but if you managed this you would also have 0.0 K in the container, so 2 for 1!

 

[Hill]

would also have 0.0 K in the container

I don't think so. If there is nothing in the container then the temperature is undefined.

 

[Chestermiller]

Thanks for all inputs, I'm following up again with some additional wonderings.Does it mean that the delta pressure forces are always acting on the pipe-walls in the same way (as stated in the first reply to my post), but in the absence of pressure the material of the walls facing lach of pressure will suffer "more" from it's internal stresses in it's chemical bonds? Or in a different sentence; without external pressure, materials are "forced less together"?

Get yourself a book on "strength of materials" to understand how pressures, stresses, and strains are related. The average of the internal and external pressures determines how much on average the molecules are forced together radially. The difference of the internal and external pressures determines how much the molecules are stretched apart in the hoop direction. The forcing together- or pulling apart of the molecules is a directional effect.

If I understood the above correctly, it kind of answers both my questions I think. Does there exist any graphs or similar that shows these effects? And does there exist some kind of issue if we raised the pressure super-high (but still with a delta P of 1.0 bar)?
Are you asking, or stating? I agree, but if you managed this you would also have 0.0 K in the container, so 2 for 1!

 

[kaare_t]

Get yourself a book on "strength of materials" to understand how pressures, stresses, and strains are related.

Thanks for the tip, will do! And also thanks for your replies!

I don't think so. If there is nothing in the container then the temperature is undefined.

I do agree with you!