Pressure in branching pipes when diameters are not equal

[fraggordon]

TL;DR Summary

Trying to solve pressure in branching pipes with non-equal diameters. Inlet flow parameters are given.

Electrical engineer here hi!

I'm little bit out of my comfort zone trying to figure out the following fluid mechanics problem. I have a branching pipe similar to schematic below...

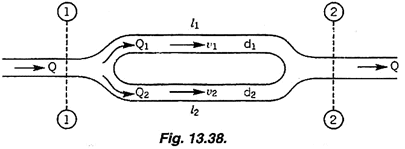
...and I'm trying to find the pressures in branches 1 (p1) and 2 (p2). The d1 and d2 are not equal (d1 = 0.1*d and d2 = 0.5*d) but the lengths l1 and l2 are equal. The inlet diameter (d), flow rate (Q), velocity (v) and pressure (p) are given.

Is it even possible to figure out the p1 and p2 with this little information? If so, where should I start? I imagine that at least following equations will be needed, but I guess I would need something else as well?

1) Conservation of flow rate: Q = Q1 + Q2
2) Conservation of energy (no losses or height difference): 0.5*density*v^2 + p = 0.5*density*v1^2 + p1 + 0.5*density*v2^2 + p2

 

[Lnewqban]

Welcome!
Pressure along each branch will change from P1 to P2 values.
That equal delta pressure is what drives each flow.
Naturally, each branch will self-balance its flow percetage according to its own restriction.

 

[jrmichler]

Is this a homework problem? If so, we can move it to the homework forum.

You can find the pressure drop from p1 to p2, then p2 if you know p1 (or vice versa).

You know the diameters, lengths, and total flow. The next step is to calculate the flow rates in the two branches subject to the conditions that the sum of those two flow rates is equal to the total flow and the pressure drops are equal. This is an iterative calculation using a Moody chart (search the term).

 

[erobz]

Electrical Engineer, no problem.

Think about this as two resistors in parallel across a DC voltage.

The pressure $P_i$ is analogous to the Voltage at node $i$

The loss of pressure in the pipe between nodes is given by $\frac{f}{lD}\frac{v^2}{2g}$

You'll want to convert from velocity to volumetric flow rate $Q$ for each branch, assuming uniform velocity distribution across each branch.

Then you will have to find the Reynolds Number, and as others have pointed out, using it determine an initial estimate for the friction factor $f$

From there you are going to get a system of equations that looks something like this:

$$ Q = Q_1 + Q_2 $$

$$ Q_1 = Q_2 k \sqrt{ \frac{f_2}{f_1} } $$

Where $k$ is a constant comprised of several parameters tied to each branch geometry.

You are going to assume a flow distribution, find the friction factors $f$ from the Moody Diagram, solve and re-evaluate $f$ based on the solutions until its change is negligible.

It appears that you are going to need some more information if you are going to actually find the pressure drop between 1 and 2. Namely one of the pressures or the total flow rate should get you there as others have pointed out.

EDIT:

Looking more carefully at your information (2) conservation of energy. Are you really to assume, no losses between section 1 and 2? If that's the case the pressure drop is trivial.

I believe you should have this instead:

$$ \frac{P_1}{\gamma} + z_1 + \frac{v_1^2}{2g} = \frac{P_2}{\gamma} + z_2 + \frac{v_2^2}{2g} + \sum_{1 \to 2 } h_l $$

Also, I'm not sure on this, but if there is no friction (inviscid flow) then the flow just splits 50/50 in each branch... regardless of actual branch diameter.

and I'm trying to find the pressures in branches 1 (p1) and 2 (p2).

The pressures in each branch will vary along their length linearly from the common pressure at their junction. So, when you say you are trying to find the "pressure in each branch", the answer is "where" not exactly a "what".