Pressure within two connected vessels

[MB613d]

Homework Statement

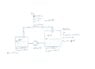
Two half with a fluid filled vessels are connected through two pipes in a closed system. The bottom pipe pumps the fluid from vessel 1 to vessel 2 at a rate of 300m³/h. The fluid pushes the air of vessel 2 through the top pipe into vessel 1. What is the pressure within the vessels? Drawing attached.

Data

Pipe:
DN = 150 mm
l = 20 m
Zeta = 15

Vessel 1:
V1 = 5.000 m³
V2_Gas = 2.500 m³

Vessel 2:
V2 = 10.000 m³
V2_Gas = 5.000m³

Overall:
p0 = pressure before the pump starts = athmospheric = 1,013 bar
T = const = 273,15 K
V1 = const
V2 = const

EDIT: In the drawing lambda should be zeta

Homework Equations

p*V=n*R*T ?

The Attempt at a Solution

I calculated the pressure drop within the pipe to be dp = 2,5 mbar.
Now I assume that when the pump starts the pressure p2 in vessel 2 will equal the pressure loss within the pipe plus p0. I use the ideal gas law to calculate the mass of the air within vessel 2 at the pressure p0 and p0+dp. I calculate the difference between the mass at p0 and p0+dp and substract it from the mass in vessel 1. Now I calculate the pressure in vessel 1 with the calculated mass.

I guess it's not right. I have spent a long time in the library to find a similar problem but couldn't find anything. I would really appreciate your help. Thank you all in advance. PS: Please excuse my english.

 

[BvU]

[edit] Oh, and: Hello MB, $\qquad$ $\qquad$ !

Apparently you need $\Delta p =$ 2.5 mBar to sustain the 300 m³/h volume flow of the gas. In V₁ the gas volume increases, so the pressure wants to drop; in V₂ the gas volume decreases, so the pressure wants to rise. As a good democrat, I would split the $\Delta p$ over the two vessels. You'll need a very good pressure meter to notice such a small deviation

 

[MB613d]

Hey BvU I guess that would be correct if both vessels had the same volume.
If I use my suggested method I get your proposed result.

Thank you for welcoming me!

 

[BvU]

if both vessels had the same volume

I see what you mean. I estimated an equal split based on the flow, but you are probably right and come to a 2:1 ratio based on the relative change in V_gas
@Chestermiller ?

 

[MB613d]

m1_p0 = 3231,13 kg (Mass of the air in vessel 1 at p0 pressure)
m2_p0 = 6462,25 kg (Mass of the air in vessel 2 at p0 pressure)
m2_p0+dp = 6478,20 kg (Mass of the air in vessel 2 at 101,55 kPa = p0+dp)

delta_m2 = (m2_p0+dp) - (m2_p0) = 15,95 kg

m1_p0 - delta_m2 = 3247,07 kg
p1 = (3247,07 kg * 287,1 [J/K*mol] * 273K) / 2500 m³ = 1,0080 kPa = 1,008 bar
287,1 [J/K*mol] = R_S,Air (Constant)
p0-p1 = - 5 mbarI just don't know If suggesting the dp as the pressure in vessel 2 is correct.
This ratio is the same as using p1*V1=p2*V2.

p1 = p2 * V2 / V1 = 2,5 mbar * 5000 m³ / 2500 m³ = 5 mbar

 

[Chestermiller]

I see what you mean. I estimated an equal split based on the flow, but you are probably right and come to a 2:1 ratio based on the relative change in V_gas
@Chestermiller ?

I don't understand what the problem is asking or what the OP did. Are you trying to find the final steady state pressures in the two vessels.

 

[MB613d]

I don't understand what the problem is asking or what the OP did. Are you trying to find the final steady state pressures in the two vessels.

Exactly! Please excuse my english.

 

[BvU]

Don't understand post #5 either (*). My curiosity was on: how is the $\Delta p$ -- needed to move the gas -- distributed over the two vessels if one is twice as big as the other.

(*) @MB613d : you originally had 1.013 Bar, now both have increased ?

 

[MB613d]

(*) @MB613d : you originally had 1.013 Bar, now both have increased ?

I used the ideal gas law to calculate the mass of the air within both vessels.
First I calculated the mass of the air at p0 = 1,013 bar for both vessels.
Then I calulated the mass of the air at po + Δp = 1,0155 bar for vessel 2 to find out how much air moves from vessel 1 to vessel 2.

I took the mass of the air which moved to vessel 2 to increase the pressure by Δp and substracted it from the mass of the air in vessel 1.
Then I calculated the pressure p1 in vessel 1 for that new mass.

I used p*V=m*R_S,Air * T for all the calculations.

The result is a pressure drop of 5 mbar in vessel 1.

 

[BvU]

how much air moves from vessel 1 to vessel 2.

But you know that 300 m3/h moves from vessel 2 to vessel 1 ! That's in the other direction!

 

[Chestermiller]

It seems to me that this is a transient problem. The pressures in the two gases will be changing with time. What does the parameter lambda stand for?

 

[MB613d]

But you know that 300 m3/h moves from vessel 2 to vessel 1 ! That's in the other direction!

I think it does not make a difference.

The pump pumps fluid from vessel 1 to vessel 2. The fluid pushes the air from vessel 2 to vessel 1. The pressure drop happens within the gas pipe from vessel 2 to vessel 1. Therefore the pressure in vessel 2 will be higher than in vessel 1.

It seems to me that this is a transient problem. The pressures in the two gases will be changing with time. What does the parameter lambda stand for?

The parameter lambda stands for resistance in the piping. Its the sum of bends and turns etc. It is used to calculate the pressure drop in the piping. I already caluclated that to be 2,5mbar.
I guess the pressure does change with time due to the inertia of the mass. But once the pump is running the pressure will be constant.

 

[Chestermiller]

The parameter lambda stands for resistance in the piping. Its the sum of bends and turns etc.
I guess the pressure does change with time due to the inertia of the mass. But once the pump is running the pressure will be constant.

Let's see your fluid flow analysis for the pipe.

 

[MB613d]

I calculated the flow speed:

w = V*4/PI() *d^2 = 4,7 m/s

Then Reynolds number:

Re = w * d * 1,29kg/m³ / 0,018 mPas = 49997 < 10^5

Blasius:
Lambda = 0,3164 / Re ^0,25 = 0,0212
Zeta = 15

delta p = (zeta + lambda*l / d) + w^2 * 1,29 kg/m³ / 2
delta p = 254 Pa = 2,54 mbar

Sorry I mixed up lambda and zeta in the original post.

 

[Chestermiller]

I calculated the flow speed:

w = V*4/PI() *d^2 = 4,7 m/s

Then Reynolds number:

Re = w * d * 1,29kg/m³ / 0,018 mPas = 49997 < 10^5

Blasius:
Lambda = 0,3164 / Re ^0,25 = 0,0212
Zeta = 15

delta p = (zeta + lambda*l / d) + w^2 * 1,29 kg/m³ / 2
delta p = 254 Pa = 2,54 mbar

Sorry I mixed up lambda and zeta in the original post.

What makes you think that the density is going to remain constant? The number of moles of gas and the volume of gas in each tank is changing with time. I guess your result is a good estimate for short times. As time progresses, the pressure difference is going to change with time.

 

[MB613d]

What makes you think that the density is going to remain constant? The number of moles of gas and the volume of gas in each tank is changing with time. I guess your result is a good estimate for short times. As time progresses, the pressure difference is going to change with time.

As the temperature is constant the density will be constant.
The ideal gas law takes the change of pressure and the moles into account. It does not use the density.
If you are relating to the calculation for the pipe, that's the standard procedure to calculate the reynolds number.

With time the gas volume in the tanks change.
How do I calculate the pressure in tank 2 without suggesting it to be athmosphere + 2,5 mbar?

This is a school homework and it does not need to be perfect.

 

[Chestermiller]

Here's my take on this:
$$n_1=\frac{p_1(V_{10}+\alpha t)}{RT}\tag{1}$$
$$n_2=\frac{p_2(V_{20}-\alpha t)}{RT}\tag{2}$$
where $\alpha=300\ m^3/h$, $V_{10}$ = gas volume in tank 1 at time zero and $V_{20}$ = gas volume in tank 2 at time zero. Since the total number of moles of gas is constant, $$p_1(V_{10}+\alpha t)+p_2(V_{20}-\alpha t)=p_0(V_{10}+V_{20})$$At short times (like you have been analyzing so far),
$$p_1V_{10}+p_2V_{20}=p_0(V_{10}+V_{20})\tag{t ---> 0}$$This is what you would use in conjunction with the pressure difference to get p1 and p2 individually.

If we take the time derivatives of Eqns 1 and 2, we obtain:$$\frac{dn_1}{dt}=\frac{(V_{10}+\alpha t)\frac{dp_1}{dt}+\alpha p_1}{RT}\tag{3}$$
$$\frac{dn_2}{dt}=\frac{(V_{20}-\alpha t)\frac{dp_2}{dt}-\alpha p_2}{RT}\tag{4}$$
Eqn. 3 gives the rate of change of the number of moles in tank 1, and this is also equal to the molar flow rate from tank 2 to tank 1. The mass flow rate from tank 2 to tank 1 is obtained by multiplying by the molecular weight M: $$\dot{m}=M\frac{(V_{10}+\alpha t)\frac{dp_1}{dt}+\alpha p_1}{RT}\tag{5}$$

The Reynolds number is given by: $$Re=\frac{4\dot{m}}{\pi D \mu}\tag{6}$$

I think I'll stop here for now and give you a chance to digest this.

 

[MB613d]

I think I'll stop here for now and give you a chance to digest this.

Thank you for your time! I'll have a look at it tomorrow morning. I'm going to bed now. Thank you!

 

[Chestermiller]

It's now pretty obvious that, since the pressures in the two vessels will initially be equal, there will be no initial flow through the intervening pipe. Instead, the pressure in vessel 2 will initially increase and the pressure in vessel 1 will initially decrease (at constant number of moles in each) as the gas in vessel 2 is compressed and the gas in vessel 1 expands at short times according to: $$p_1=\frac{p_0V_{10}}{(V_{10}+\alpha t)}$$
$$p_2=\frac{p_0V_{20}}{(V_{20}-\alpha t)}$$
Once a small pressure difference is established across the pipe, gas begins flowing.

 

[MB613d]

Once a small pressure difference is established across the pipe, gas begins flowing.

Thank you for your answer.
I understand what you did there and I think it is correct.

So do you think the pressure loss of the pipe is the pressure that needs to be established before gas begins to flow?

 

[Chestermiller]

Thank you for your answer.
I understand what you did there and I think it is correct.

So do you think the pressure loss of the pipe is the pressure that needs to be established before gas begins to flow?

If you understand what I am saying, then you know that this is a totally transient problem, and that there is no steady state. The initial pressure difference between the two vessels is zero, and thus the initial mass flow rate through the pipe is zero. As time progresses, the pressure difference between the vessels and the mass flow rate through the pipe both increase gradually with time. So there is no magic pressure difference at which the gas starts flowing.

The mistake in your original analysis was assuming that the volume flow rate of gas through the pipe must match the volume flow rate of water between the two vessels. Because the air is compressible, this is not the case. The equations I gave in post #19 show how the pressures vary at short times when there is not enough of a pressure difference across the pipe to produce significant air flow.

So, initially, the flow Reynolds number is zero, and it builds up gradually with time, first passing through the laminar region, then the transition, and then to turbulent flow at later times.

The flow analysis would go something like the following if the zeta resistances were distributed uniformly along the length of the pipe: At any given time, the pressure gradient in the pipe would be $$\frac{dp}{dz}=-\left[\frac{\zeta}{L}+\frac{\lambda(Re)}{D}\right]\frac{1}{2}\rho w^2\tag{1}$$where $p=p_2$ at z = 0 and $p=p_1$ at z = L and Re is given by Eqn. 6 in post #17. The mass flow rate through the pipe is given by: $$\dot{m}=\rho wA\tag{2}$$where, from Eqn. 5 in post #17,
$$\dot{m}=\frac{M}{RT}\frac{d[p_1(V_1+\alpha t)]}{dt}\tag{3}$$
If we combine Eqns. 1 and 2, we obtain:$$\frac{dp}{dz}=-\left[\frac{\zeta}{L}+\frac{\lambda(Re)}{D}\right]\frac{1}{2}\frac{(\dot{m})^2}{\rho A^2}\tag{4}$$From the ideal gas law, the density is given by: $$\rho=\frac{pM}{RT}$$Substituting this into Eqns. 4 then yields:
$$p\frac{dp}{dz}=-\left[\frac{\zeta}{L}+\frac{\lambda(Re)}{D}\right]\frac{1}{2}\frac{RT(\dot{m})^2}{M A^2}\tag{5}$$Next, integrating this equation between z = 0 and z = L yields:$$p_2^2-p_1^2=\left[\zeta+\lambda(Re)\frac{L}{D}\right]\frac{RT(\dot{m})^2}{M A^2}\tag{6}$$It follows from an un-numbered equation in post # 17 that $p_2$ can be expressed in terms of $p_1$ as:
$$p_2=p_0+\frac{(V_{10}+\alpha t)}{(V_{20}-\alpha t)}(p_0-p_1)\tag{7}$$$p_2$ can be eliminated from Eqn. 6 by substitution of Eqn. 7 to yield:
$$\left(p_0+\frac{(V_{10}+\alpha t)}{(V_{20}-\alpha t)}(p_0-p_1)\right)^2-p_1^2=\left[\zeta+\lambda(Re)\frac{L}{D}\right]\frac{RT(\dot{m})^2}{M A^2}\tag{8}$$Since the Reynolds number Re is a function of $\dot{m}$, Eqn. 8 is of the mathematical form $$g(p_1,t)=f(\dot{m})\tag{9}$$If we formally invert this to solve for $\dot{m}$ and combine the result with Eqn. 3, we obtain: $$\frac{d[p_1(V_1+\alpha t)]}{dt}=\frac{RT}{M}h(p_1, t)\tag{9}$$
Integrating this ordinary differential equation with respect to time allows us to determine $p_1$ as a function of time.

 

[MB613d]

I see now.
This is turning into a very complicated problem and its above my mathematical knowledge.
All I want is to find out the maximum pressure.
When do you think the pressure would me at a maximum?

When the pump is running on full speed and the gas volume of V2 is at its lowest point?Thank you so much for your post. I am trying to understand.

 

[Chestermiller]

I see now.
This is turning into a very complicated problem and its above my mathematical knowledge.
All I want is to find out the maximum pressure.
When do you think the pressure would me at a maximum?

When the pump is running on full speed and the gas volume of V2 is at its lowest point?Thank you so much for your post. I am trying to understand.

I think you mean that you are trying to find the maximum pressure difference, right? What is the exact statement of the problem (translated into English, of course)?

 

[MB613d]

The task is as follows:
Determine the maximum pressure in tank 2 due to filling.

I'm totally confused.

 

[Chestermiller]

The task is as follows:
Determine the maximum pressure in tank 2 due to filling.

I'm totally confused.

It isn't clear to me either. I haven't figured out yet how to solve for the maximum value of p2 during filling without solving the complicated differential equation. The problem is the volume terms that are changing with time.

 

[Chestermiller]

This problem has got me pissed off. I think I'm going to solve it numerically (say for the simpler case of zeta = 0), and see what the solution looks like. Keep you posted.

 

[MB613d]

I feel you.. I've spent nearly two weeks now trying to solve it.
It's above my knowledge and I tried to find similar problems in the library but couldn't find anything.

I appreciate your help and I'm really happy about that.

 

[Chestermiller]

I analyzed the case where zeta is neglected and, for the parameters in this problem, came up with the following ordinary differential equation:
$$\frac{d[P_1(V_{10}+\alpha t)]}{dt}=-\alpha+5.27(P_2-P_1)^{4/7}$$where $P_1=\frac{p_1}{p_o}-1$, $P_2=\frac{p_2}{p_o}-1$, $V_{10}$ is in m^3, t is in seconds, and $\alpha =\frac{1}{12}\ \frac{m^3}{sec}$.

The numerical solution to this equation, shown in the figure below, indicates that that the system approaches quasi steady state very rapidly (within two seconds). In the case of this figure, since we assumed zeta is negligible, the final quasi static pressure difference between the two chambers is predicted to be only 0.7 mBar, compared to 2.54 mBar when zeta is not neglected.

Physically, the term quasi static means that the flow resistance of the pipe is very low, and that the pressures in the two chambers will be nearly equal at all times. So the present analysis provides mathematical justification for the approximation that you made in your original post that (a) the volumetric flow rate in the pipe is essentially 300 m^3/hr and (b) the density of the air does not vary significantly from 1.29 kg/m^3. This led to the result that $$p_2-p_1=0.00254\ bars\tag{1}$$
Even though the pressure difference between the two chambers rapidly reaches a constant value, the individual pressures in the two chambers will vary with time t. These individual pressures at any time t can be determined by solving Eqn. 1 simultaneously with the equation:
$$p_1(V_{10}+\alpha t)+p_2(V_{20}-\alpha t)=p_0(V_{10}+V_{20})\tag{2}$$where po is 1.013 bars.

What do you get when you solve this at t = 0? What do you get when you solve this at t = 30 sec (the time when tank 1 becomes empty)?

I guess that it is best to report the pressures in the tanks as gauge pressures (to avoid roundoff in the answers).