Principle of Virtual Work and the forces that DO NOT do work

Click For Summary

Discussion Overview

The discussion revolves around the application of the Principle of Virtual Work (PVW) in a planar linkage system, specifically focusing on how to determine reaction forces that do not perform work. Participants explore the methodology for calculating these forces after applying PVW, and the challenges associated with it.

Discussion Character

  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant describes a scenario involving motors and gravity in a 2D linkage system, stating that four reaction forces do not do work and expresses confusion about how to calculate these forces after applying PVW.
  • Another participant questions the simplicity of the original query, suggesting that the solution might be straightforward but does not elaborate on what that solution is.
  • A later reply clarifies that the initial confusion was about obtaining reaction forces at the base and between arms, which was resolved through the application of Newton's third law and a series of equations.
  • One participant notes the existence of an alternative method using Lagrange multipliers to account for constraints but admits to a lack of experience with that approach.
  • There is a sentiment expressed that many textbooks fail to provide a systematic method for calculating reaction forces after applying PVW, which adds to the confusion for learners.

Areas of Agreement / Disagreement

Participants express varying levels of confidence in the simplicity of the solution to the problem, with some feeling that the question was trivial while others acknowledge the complexity involved in determining the reaction forces.

Contextual Notes

Participants highlight the limitations of existing literature in providing clear methodologies for calculating reaction forces after applying PVW, indicating a gap in instructional resources.

Trying2Learn
Messages
375
Reaction score
57
TL;DR
How do you get the reaction forces that do no work
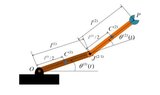
In this 2D figure below, I can place:

  • a motor at O
  • a motor at J
  • gravity on each link

I can use Hamilton's principle, modified to the principle of virtual work and I can compute the motion of the linkage system.

I do not have to account for these force FOUR forces (in this planar problem):
  1. 2 Reaction forces at O (they do no work)
  2. 2 Reaction forces at J (they do no work)
I have no difficulty with the previous work, above... The next part, counfounds me, and I ask for help.

However, how would I find those four reaction forces that do no work?

Would I first have to solve the entire problem using PVW, get the velocity, acceleration, angular velocity and angular acceleration?

And then, return to free body diagrams, and with the kinematics and inertial terms (mass and moment of inertia), go back and mathematically deduce what those forces SHOULD be?

How does software do it?

I have never seen a textbook discuss this. They just blithely (sometimes smugly) pronounce the power of PVW as being able to ignore forces that do no work (which is true and wonderful), but they never present a systematic way to go back and get those other forces that do no work.UNLESS: they enter as constraints, brought in by Lagrange multipliers. If so, then I must research that, alone (before bothering any of you--you have all been patient). However, in the absence of having to use that formality, how would YOU solve for these reaction forces that do no work? Can someone start me off so that I can then teach myself the Lagrange multipliers?
 

Attachments

  • PVW.JPG
    PVW.JPG
    8.8 KB · Views: 185
Last edited:
Physics news on Phys.org
I have changed my mind. This is a stupid question and the solution is simple. I am sorry for having wasted the time of some of you.
 
Trying2Learn said:
This is a stupid question and the solution is simple.
Why?
What that simple solution would be?
 
Lnewqban said:
Why?
What that simple solution would be?
Oh

THE FIRST PART: is that I use Principle of Virtual Work (PVW and calc.variations) and Generalized coordinates, and I find the angles and the motion. That was not my issue, though.

MY issue was now to get the reaction forces at the base, and between the two arms.

I was confused.

So I spent some time...

I cut the body up using Newton's third law (action and reaction) and get a series of equations for the support reaction forces and the interaction forces and I solved those, and I was done.

------------------------

I KNOW that it can ALSO be done by infusing the constraints directly with Lagrange multipliers, but I have never done that before.

What irritated me, is that most books just blithely state "we can solve for the motion by PVW since the reaction forces can be ignored (they do not work); but no book (at least the ones I have seen), takes the next step and shows you (Either by Free body Diagrams or Lagrange Multipliers) how to get the reactions.
 
Last edited:
Reply
  • Like
Likes   Reactions: Lnewqban

Similar threads

Graduate Virtual work of constraint forces in Hamilton’s principle
  • · Replies 7 ·
Replies
7
Views
1K
Graduate Hamilton's principle and virtual work by constraint forces
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Virtual work and constraint forces
  • · Replies 1 ·
Replies
1
Views
2K
Graduate Principle of virtual work for continuous systems
  • · Replies 5 ·
Replies
5
Views
2K
Graduate Uncovering the Motivation behind the Principle of Virtual Work
  • · Replies 6 ·
Replies
6
Views
3K
Undergrad Why does the Principle of Virtual Work work without higher math?
  • · Replies 7 ·
Replies
7
Views
2K
Graduate Virtual work and D'alembert's principle
  • · Replies 4 ·
Replies
4
Views
4K
Graduate D'Alembert's principle and the work done by constraint forces
  • · Replies 6 ·
Replies
6
Views
3K
Principle of Virtual Work to the FE method
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Virtual displacement is not consistent with constraints
  • · Replies 3 ·
Replies
3
Views
2K