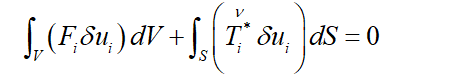Trying2Learn
- 375
- 57
- TL;DR Summary
- PVW, FE, Equilibrium Equations
(I do understand there are many ways to formulate the FE method, but I wish to understand this one.)
HOWEVER
If my focus was ONLY the PVW alone, I can understand this and where it came from: both are forces acting through virtual displacements)
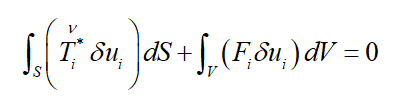
But the development of the FE equations give (when we apply Gauss theorem, definition of strain, etc.)
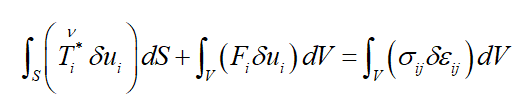
Now, I can anticipate that this new term on the right is the INTERNAL virtual work: stress and variation of strain, internal
However, it seems so ad hoc, that books get away with this.
It seems to me that this statement below is CRITICAL:
When the Internal virtual work is equal to the External Virtual work, we recover the equilibrium equation and the boundary condition.
It seems to me that this BOLD statement above is the beating heart of the FE method (from the mechanical engineering perspective), but all books give it lip service and appear to simply "tweak" the PVW and "add this term."
I am sorry to say I am not entirely sure of where my confusion lies, but it seems to be that the BOLD BLUE statement above, must rise above the development and must become a restatement of the PVW.
I do not know what I am trying to ask, but could someone comment on this post?
Maybe I am beating this, senseless.
- I understand that Hamilton's Principle is just that: a principle ( a law the recapitulates the equations of motion)
- I also understand that the Principle of Virtual Work (PVW) is a reformulation of Hamilton's Principle to account for non-conservative forces (in bodies that are rigid)
HOWEVER
If my focus was ONLY the PVW alone, I can understand this and where it came from: both are forces acting through virtual displacements)
But the development of the FE equations give (when we apply Gauss theorem, definition of strain, etc.)
Now, I can anticipate that this new term on the right is the INTERNAL virtual work: stress and variation of strain, internal
However, it seems so ad hoc, that books get away with this.
It seems to me that this statement below is CRITICAL:
When the Internal virtual work is equal to the External Virtual work, we recover the equilibrium equation and the boundary condition.
It seems to me that this BOLD statement above is the beating heart of the FE method (from the mechanical engineering perspective), but all books give it lip service and appear to simply "tweak" the PVW and "add this term."
I am sorry to say I am not entirely sure of where my confusion lies, but it seems to be that the BOLD BLUE statement above, must rise above the development and must become a restatement of the PVW.
I do not know what I am trying to ask, but could someone comment on this post?
Maybe I am beating this, senseless.