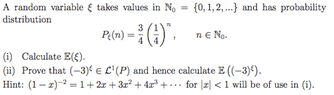- #1
Carla1985
- 94
- 0
I'm stuck on this question. I've done plenty of the questions with numbers etc but not sure how to deal with the n case for this one.
View attachment 689
Thank you :)
View attachment 689
Thank you :)