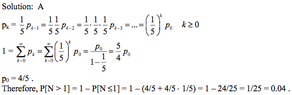- #1
schinb65
- 12
- 0
In modeling the number of claims filed by an individual under an automobile policy
during a three-year period, an actuary makes the simplifying assumption that for all
integers n ≥ 0, $p_n+1 = \frac{1}{5} p_n$ , where $p_n$ represents the probability that the policyholder files $n$ claims during the period.
Under this assumption, what is the probability that a policyholder files more than one
claim during the period?
So my question is the solution which I have attached. How do we go from
$\sum_{k=0}^{\infty}\frac{1}{5}^kp_0$ to the next step $\frac{p_0}{1-\frac{1}{5}}$
Thank you.
during a three-year period, an actuary makes the simplifying assumption that for all
integers n ≥ 0, $p_n+1 = \frac{1}{5} p_n$ , where $p_n$ represents the probability that the policyholder files $n$ claims during the period.
Under this assumption, what is the probability that a policyholder files more than one
claim during the period?
So my question is the solution which I have attached. How do we go from
$\sum_{k=0}^{\infty}\frac{1}{5}^kp_0$ to the next step $\frac{p_0}{1-\frac{1}{5}}$
Thank you.