nacho-man
- 166
- 0
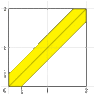
Alice and bob each choose a number at rndom between zero and two. We assume a uniform probability law under which the probability of an event is proportional to it sarea. Consider the following events:
A: The magnitude of the difference of the two numbers is greater than 1/3
B: At least one of the numbers is greater than 1/3
C: The two numbers are equal
D: Alice's number is greater than 1/3
So, find $ P(A), P(B), P(A\cap B) , P(C), P(D), P(A\cap D)$
A: The magnitude of the difference of the two numbers is greater than 1/3
B: At least one of the numbers is greater than 1/3
C: The two numbers are equal
D: Alice's number is greater than 1/3
So, find $ P(A), P(B), P(A\cap B) , P(C), P(D), P(A\cap D)$