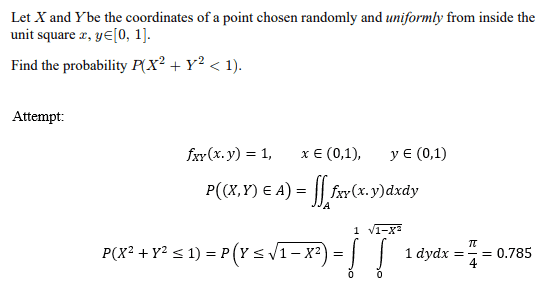Probability/Random variables question

[ashah99]

Homework Statement

Finding the probability of randomly choosing a point within the unit square constrained within the quarter circle

Relevant Equations

P(( X, Y ) ∈ A) = ∫∫ fXY ( x, y )dxdy

Hello all, I am wondering if my approach is coreect for the following probability question? I believe the joint PDF would be 1 given that the point is chosen from the unit square. To me, this question can be reduced down to finding the area of 1/4 of a circle with radius 1. Any help is appreciated!

 

[PeroK]

It's clear from your calculations that you are indeed simply calculating the area. Which is what you would expect for a uniform distribution.

 

[ashah99]

It's clear from your calculations that you are indeed simply calculating the area. Which is what you would expect for a uniform distribution.

Ok, makes sense. Would you agree that my answer is correct? Just want to make sure I understand.

 

[PeroK]

Ok, makes sense. Would you agree that my answer is correct? Just want to make sure I understand.

Yes, it's just a ratio of areas, as you've calculated.

 

[pasmith]

Or use polar coordinates: <br /> \int_0^1 \int_0^{\sqrt{1-x^2}} 1\,dy\,dx = \int_0^{\pi/2}\int_0^1 r\,dr\,d\theta.