- #1
LCDF
- 15
- 0
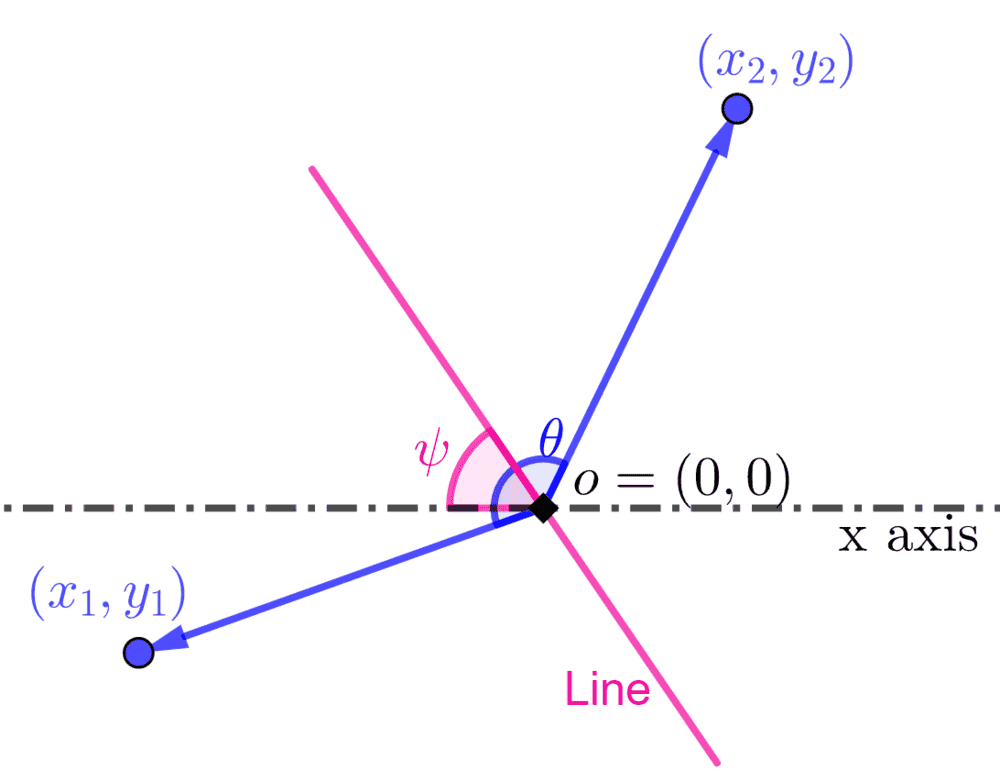
I want to find the probability that the two points ($x_1, y_1$) and ($x_2, y_2$) lie on the opposite sides of a line passing through the origin $o = (0, 0)$ and makes an angle $\psi$ that is uniformly distributed in $ [0, \pi]$ with the $x$ axis when the angle is measured in clockwise direction. The angle between the two vectors corresponding two points $(x_1, y_1)$ and ($x_2, y_2$) is $\theta$ in clockwise direction. The angle $\theta$ has the probability density function $f_{\theta}(\rho)$ for $\theta \in (0, 2\pi)$. I have
Last edited: