Probability using combinations or alternatives

[njh]

Homework Statement

52 cards, choose 4, what is the probability of getting 2 Aces and 2 Kings (in any order)

Relevant Equations

Denominator is the number of combinations of picking 4 cards out of 52, counting different orders of dealing the same 4 cards as different permutations but one single "combination": 52!/ (4! x (52-4)!) = 6,497,400/ 24 = 270,725 different combinations of 4 cards.

Numerator is the number of different ways to pick 2 Aces (out of 4 Aces in a deck) and 2 Kings (out of 4 Kings in a deck). Combination probability is "4 Choose 2": 4!/ (2! x (4-2)!) = 6

Multiply Numerator to account for 2 selections (2 of 4 Aces x 2 of 4 Kings) 6 x 6 = 36.

Probability of 4 cards being drawn out of 52 and those cards being 2 Aces and 2 Kings is 36/ 270,725 = 0.133%.

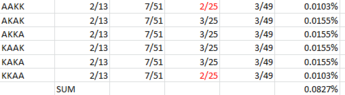
I have attempted the solution above and I am fairly sure that it is correct. My question is the following: What am I calculating if I multiply 4/52 x 3/51 x 4/50 x 3/49 = 144/ 6,497,400 = 0.002%.

I got the correct answer by following the principles of combination probabilities, but intuitively I would have thought that drawing the 4 cards as I do above should result in the same answer. So I do not know what the 0.002% probability represents.

Thank you if anybody has a suggestion.

 

[PeroK]

I have attempted the solution above and I am fairly sure that it is correct. My question is the following: What am I calculating if I multiply 4/52 x 3/51 x 4/50 x 3/49 = 144/ 6,497,400 = 0.002%.

The first card can be any Ace or King, so that's $\frac{8}{52}$. The second card can be any other Ace or King, so that's $\frac 7 {51}$. After that it gets trickier. Can you see why?

 

[njh]

Thank you for prompting me to think about it that way. For the first two cards, I do not mind if I get an Ace or King, but by the third card I do mind. In a scenario where my first two cards are both Aces, then I no longer want another Ace. I only want two Kings. In that situation, it would be 8/52 * 7/51 * 4/50 * 3/49. However, that does not solve my problem, so perhaps you are hinting at another solution. This is just one scenario where I have assumed the first two cards drawn were both Aces. If I had drawn an Ace and a King, then the probability of the third card being drawn would be P( Ace or King), so 6/50. Let me go away and think about this a bit more. Thank you for the initial prompt.

 

[PeroK]

Thank you for prompting me to think about it that way. For the first two cards, I do not mind if I get an Ace or King, but by the third card I do mind. In a scenario where my first two cards are both Aces, then I no longer want another Ace. I only want two Kings. In that situation, it would be 8/52 * 7/51 * 4/50 * 3/49. However, that does not solve my problem, so perhaps you are hinting at another solution. This is just one scenario where I have assumed the first two cards drawn were both Aces. If I had drawn an Ace and a King, then the probability of the third card being drawn would be P( Ace or King), so 6/50. Let me go away and think about this a bit more. Thank you for the initial prompt.

Yes, so you need a probability tree (for example), where after two cards we have two scenarios:

AA (or KK)

AK (or KA)

You then have to treat these cases separately. You must also ask whether these two scenarios are equally likely?

 

[njh]

Thank you for that direction by phrasing the probability as 8/52 rather than 4/52. The result was surprising.

I first reviewed the Aces and Kings independently of each other, which resulted in the probability of success being the same (table below). This shows me that there is a commutative property to this calculation, which is not a surprise. It was useful in highlighting to me that in my original question I was creating one possible scenario, which was P(KKAA) = (4x3x4x3). This is just one Permutation of the 4 cards, with there being 6 possible Permutations. So, I am using the probability of one Combination for the numerator. In contrast, for the denominator in my original question (52 x 51 x 50 x 49) I am considering all Permutations possible in the deck of cards. My conclusion is that my original calculation shows me nothing of value, since I am not comparing like with like. So that answers my initial question, I think.

I still should be able to adapt my probabilities to get the same answer as I did using combinations (i.e. 36/ 270,715 = 0.133% probability of choosing two Aces and two Kings by dealing 4 cards out of 52).

What surprised me was that I did not get the same probabilities when I combined the probabilities of Aces OR Kings i.e. 8/52 for the first draw. I now see that when drawing the third card, the prior cards drawn impact the probability of what the third card can be. So, by picking two Aces or two Kings as your first two cards, you lose the optionality of the third card being either an Ace OR a King. I was missing that out initially.

So I now recognise that I need to look at the cards in combination (8/52, not 4/52). Also, I need to consider all permutations of the four cards in the numerator, since I am considering all permutations in the denominator.

I still find myself hitting a wall however: I thought that if I sum the 6 probability scenarios, then I would come to the correct answer for the probability of drawing two Aces and two Kings. This would lead me to conclude the probability is 0.0827% (i.e. 0.0414% * two, so that I consider Permutations and not Combinations e.g. AAKK and KKAA etc.).

May I check if I have made an error up to this point please? Thank you in advance for any direction.

AAKK	4/52​	3/51​	4/50​	3/49​	0.0022%​
AKAK	4/52​	4/51​	3/50​	3/49​	0.0022%​
AKKA	4/52​	4/51​	3/50​	3/49​	0.0022%​
	SUM				0.0066%​
AAKK	8/52​	7/51​	4/50​	3/49​	0.0103%​
AKAK	8/52​	7/51​	6/50​	3/49​	0.0155%​
AKKA	8/52​	7/51​	6/50​	3/49​	0.0155%​
	SUM				0.0414%​

 

[PeroK]

The method I hinted at above is that we have two cases.

Case 1: first two cards the same, with probability $\frac 8 {52}\times \frac 3 {51}$

Case 2: first two cards different, with probability $\frac 8 {52}\times \frac 4 {51}$

Then finish things off from there.

With your method, all options have the same probability. It's a good exercise to justify this.

The first half of your table is correct, the bottom half is wrong.

 

[njh]

So, I don't expect you to change your response from last time, but I do have a question. I have replicated what I did in a long form:

1. I think that for the first two cards, I do not mind whether I pick an Ace or King. Correct?
2. When I draw cards 3 and 4, the probabilities vary, depending upon whether my first two cards were the same (AA or KK) or different. Correct?

So, if I am making an error, it is with the probabilities that I am assigning to drawing an Ace or a King for cards 3 and 4?

Thankyou.

AAKK	8/52​	7/51​	4/50​	3/49​	0.0103%​
AKAK	8/52​	7/51​	6/50​	3/49​	0.0155%​
AKKA	8/52​	7/51​	6/50​	3/49​	0.0155%​
KAAK	8/52​	7/51​	6/50​	3/49​	0.0155%​
KAKA	8/52​	7/51​	6/50​	3/49​	0.0155%​
KKAA	8/52​	7/51​	4/50​	3/49​	0.0103%​
	SUM				0.0827%​

 

[pbuk]

So, if I am making an error, it is with the probabilities that I am assigning to drawing an Ace or a King for cards 3 and 4?

No, your error is that you are conflating two different methods of getting to the same result. In the first line of your table you have written "AAKK" so you want the probability of the first card being an ace. Why have you written 8/52 as the probability for the first card?

Edit: And in your spreadsheet probability tree you have written the correct probabilities in the box for each card (the red numbers outside boxes are irrelevant). Why have you not multiplied 4 x 3 x 4 x 3 / 52 x 51 x 50 x 49 for the first line?

 

[vela]

It was useful in highlighting to me that in my original question I was creating one possible scenario, which was P(KKAA) = (4x3x4x3). This is just one Permutation of the 4 cards, with there being 6 possible Permutations. So, I am using the probability of one Combination for the numerator. In contrast, for the denominator in my original question (52 x 51 x 50 x 49) I am considering all Permutations possible in the deck of cards. My conclusion is that my original calculation shows me nothing of value, since I am not comparing like with like. So that answers my initial question, I think.

I wouldn't say it's of no value. Consider this:
$$\frac{\binom{4}{2}\binom{4}{2}}{\binom{52}{4}} = \frac{\frac{4\times3}{2\times 1}\cdot\frac{4\times 3}{2\times 1}}{\frac{52\times 51\times50\times 49}{4\times 3\times 2\times 1}} = \frac{4!}{2!\,2!}\cdot\frac{4\times 3\times 4\times 3}{52\times 51 \times 50 \times 49}$$ In your second approach, you calculated the second factor but forgot the first to get the total probability.

 

[njh]

Thank you for that.

It helped me realise that I made an error in my Combination calculation at the start and I have since been trying to magic a probability-derived answer that fit with this incorrect calculation. How very frustrating. I now see that 36/ 270,725 equals 0.013% and not 0.133%, so I can start again and try and get the right answer using probabilities. Thanks again.

 

[njh]

No, your error is that you are conflating two different methods of getting to the same result. In the first line of your table you have written "AAKK" so you want the probability of the first card being an ace. Why have you written 8/52 as the probability for the first card?

Edit: And in your spreadsheet probability tree you have written the correct probabilities in the box for each card (the red numbers outside boxes are irrelevant). Why have you not multiplied 4 x 3 x 4 x 3 / 52 x 51 x 50 x 49 for the first line?

Thank you for that.

So, my first mistake was in my original Combination calculation that I thought I had correct. I calculated 36/ 270,725 as equal to 0.133%, whereas it is 0.0133%. In trying to replicate the same wrong answer using probabilities I ignored logic and tried magic and brute force instead.

I take your point that I tried using two different methods of calculation in the same table. My logic was that for the first two draws I do not mind whether I get an Ace or King, so the probability is 8/52 x 7/52 (any Ace or King will do). Then, in the example of drawing AAKK, I can only draw a King for the third card and a King or the fourth card, so I used the probability 4/50 * 3/49. So, that would be P(Ace or King) * P(Ace or King) * P(King) * P(King). I believe that this is wrong because I am confusing random probabilities P(Ace or King) with specific outcomes P(AAKK).

Having determined that there are 6 possible ways to draw two Aces and two Kings, then having listed them, I should have calculated the probability of each of those specific outcomes. So, in the case of P(AAKK) it is P(Ace) * P(Ace) * P(King) * P(King), not P(Ace or King). I then sum the probabilities to get 0.0133%.

The correct table is below, along with the long version. I am a little cautious still of saying that I have got the method of this correct, even though the answer is 0.0133% probability of drawing any two Aces and two Kings out of 52 cards using either method. If you could confirm that I have this correct, it would be appreciated. Incidentally, I assume that I could also have calculated this starting with P(Ace or King = 8/52) instead of P(King = 4/52), but I would have had to change the process for cards 3 and 4? Thank you.

The reason that I did not get the correct answer with (4 x 3 x 4 x 3)/ (52 x 51 x 49 x 48) is because I was calculating the probability of only one event, such as P(AAKK), in the numerator. In contrast, in the denominator I was calculating the probability of every permutation of drawing 4 cards out of 52, in every different order. I should have multiplied the numerator by 6, converting the single permutation into a Combination; or divided the denominator by 6, to do the reverse.

AAKK	4/52​	3/51​	4/50​	3/49​	0.0022%​
AKAK	4/52​	4/51​	3/50​	3/49​	0.0022%​
AKKA	4/52​	4/51​	3/50​	3/49​	0.0022%​
KAAK	4/52​	4/51​	3/50​	3/49​	0.0022%​
KAKA	4/52​	4/51​	3/50​	3/49​	0.0022%​
KKAA	4/52​	3/51​	4/50​	3/49​	0.0022%​
	SUM				0.0133%​

 

[WWGD]

P(King) is the capital of China, last I checked ;).

 

[njh]

Very amusing!