Problem of spring block system: force vs conservation of energy

[ShaunPereira]

Homework Statement

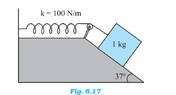
A 1 kg block situated on a rough incline is connected to a spring of spring constant 100
N m–1 as shown in Fig. 6.17. The block is released from rest with the spring in the
unstretched position. The block moves 10 cm down the incline before coming to rest.
Find the coefficient of friction between the block and the incline. Assume that the
spring has a negligible mass and the pulley is frictionless.

Relevant Equations

F=ma
work energy theorem
-1/2kx^2 - umcosΘx +umgsinΘx = 0

I have used the work energy theorem like all source have shown me an have arrived at the right answer
where work one by all the forces is the change in kinetic energy
-1/2kx^2 - umgcosΘx +mgsinΘx = 0 is the equation
which becomes

-1/2kx -umgcosΘ+ mgsinΘ = 0
where k= spring constant
u= coefficient of friction
m=mass x= extension of spring and theta is the angle of inclination
there is no change in KE so it is zero

My problem is that can't we find the same result ( find u) with Newtons second law

my attempt at this is

-kx -umgsinΘ+umgcosΘ =ma when the spring is stretched and the body is at rest
since the body is at rest i have assumed a to be zero ( it could be non zero, i don't know.)

that gives us -kx -umgcosΘ +umgsinΘ = 0
if you compare this equation with the equation in red above you notice a factor of 1/2 missing from the term kx which bothers me

I am surely doing something wrong while using Newtons second law but i don't know what it is

A little help would be appreciated

 

[Steve4Physics]

Hi @ShaunPereira. Are you familiar with the coefficient of kinetic friction and the coefficient of limiting static friction? If not, do a little background reading.

Think about how you could determine each type of coefficient for the sort of system you describe.

 

[ShaunPereira]

Hi @ShaunPereira. Are you familiar with the coefficient of kinetic friction and the coefficient of limiting static friction? If not, do a little background reading.

Think about how you could determine each type of coefficient for the sort of system you describe.

The coefficient of static friction is the one we take into account when a body is at rest and the coefficient of kinetic friction is what we take into account when a body is moving ( this is my rudimentary understanding of it)SO do you mean to say that the equation in red gives us the coefficient of kinetic friction and the equation in green gives us the coefficient of static friction?

 

[haruspex]

-kx -umgsinΘ+umgcosΘ =ma when the spring is stretched and the body is at rest

I assume you meant $-kx -mg\sinΘ+umg\cosΘ =ma$. That finds a position where the block will just about remain at rest, rather than slip down, if placed there carefully, and if u is the static coefficient. It does not take into account that the body had momentum before coming to rest, so will surely overshoot that position.
Indeed, it is not immediately clear what the frictional force will be when it comes to rest, nor even the direction in which it will act.
If you want to solve it using Newton II, you will need to write the differential equation of its motion and solve that; but that will simply produce the energy equation.

The coefficient of static friction is the one we take into account when a body is at rest and the coefficient of kinetic friction is what we take into account when a body is moving ( this is my rudimentary understanding of it)

Not exactly. It's kinetic friction if the two surfaces are moving relative to each other, static otherwise. E.g. a car tyre on road has static friction unless the car is skidding.

 

[Steve4Physics]

So do you mean to say that the equation in red gives us the coefficient of kinetic friction

Yes. I guess this is what the question is asking for. It isn't possible to find the coefficient of limiting static friction from the information given.

and the equation in green gives us the coefficient of static friction?

No. Your green equation would only give the coefficient of limiting static friction (μₛ) if the stationary block were about to start sliding downhill, e.g. if m is large and you carefully set up the system so the block is stationary and on the verge of starting to slip downhill (which would stretch the spring more).

Of course, you could have a situation where the stationary block is about to start sliding uphill. That would require you to change your green equation.

Remember,, when an object is stationary on a rough slope but not on the point of slipping, the frictional force is less than its maximum (limiting) value. To find μₛ requires the object to be on the point of slipping.

Edit: typo's corrected.

 

[ShaunPereira]

Yes. I guess this is what the question is asking for. It isn't possible to find the coefficient of limiting static friction from the information given.No. Your green equation would only give the coefficient of limiting static friction (μₛ) if the stationary block were about to start sliding downhill, e.g. if m is large and you carefully set up the system so the block is stationary and on the verge of starting to slip downhill (which would stretch the spring more).

Of course, you could have a situation where the stationary block is about to start sliding uphill. That would require you to change your green equation.

Remember,, when an object is stationary on a rough slope but not on the point of slipping, the frictional force is less than its maximum (limiting) value. To find μₛ requires the object to be on the point of slipping.

Edit: typo's corrected.

Oh I get you now
Coefficient of static friction- when body is at rest ( just rest)
Coefficient of limiting static friction - when body is just about to slide
Coefficient of kinetic friction - when body is moving

The question here deals with kinetic friction which we can find by energy conservation.

However we can also use the equation in green to find the coefficient of limiting static friction

Right?

 

[kuruman]

However we can also use the equation in green to find the coefficient of limiting static friction

Right?

Not necessarily. Please read again post #5 by @Steve4Physics (paragraph that starts with "No") to see under what conditions you can use the green equation.

 

[haruspex]

Not necessarily. Please read again post #5 by @Steve4Physics (paragraph that starts with "No") to see under what conditions you can use the green equation.

And as I noted in post #4, the green equation has a spurious extra 'u' in it.

 

[ShaunPereira]

Not necessarily. Please read again post #5 by @Steve4Physics (paragraph that starts with "No") to see under what conditions you can use the green equation.

so the green equation would change depending on the direction of imminent motion and so the limiting static friction would change its direction accordingly and thus changing the sign of the term umgsinΘ (it would be negative were it acting up the incline and positive were it acting down the incline)

as for

And as I noted in post #4, the green equation has a spurious extra 'u' in it.

as you and others have rightly pointed out the u in the green equation is not the same as the u in the red equation. I would then happily change the u to any letter of your liking ,say "z".

In conclusion the green equation which now becomes

-kx (+/-) zmgcosΘ +mgsinΘ =0
where z= coefficient of limiting static friction

This equation accounts for the assumption that the system is carefully set up in a way that the block can move in either direction (if the mass is sufficiently large it will slide down and if it is not the spring force will pull it up the incline ) and the direction of limiting static friction would thus depend and hence the (+/-) in the equation

Is this correct?

 

[haruspex]

as you and others have rightly pointed out the u in the green equation is not the same as the u in the red equation

That is not my point. Look carefully at it. You have a factor u in both terms; it should only be in one of them.

 

[ShaunPereira]

That is not my point. Look carefully at it. You have a factor u in both terms; it should only be in one of them.

Yes. Sorry about that. Didn't pay attention.
I have corrected that equation and explained my thinking behind it.

Is that correct?

 

[haruspex]

Yes. Sorry about that. Didn't pay attention.
I have corrected that equation and explained my thinking behind it.

Is that correct?

Corrected it where? In post #1 I still see -kx -umgcosΘ +umgsinΘ = 0.

 

[ShaunPereira]

Corrected it where? In post #1 I still see -kx -umgcosΘ +umgsinΘ = 0.

I meant to say that I corrected it in a subsequent post namely post # 9
I will correct it in the original post too.
I am new to this forum and quite clearly don't know how everything works so will it will evidently take me some time to learn. Apologies for that.

But what I am asking is if the post I made which is post #9 and the understanding behind it is correct or not?

 

[ShaunPereira]

I just checked and there seems to be no way I can edit out the error in post #1
Posts can only be edited or deleted within a 24 hour window
Since I made the post on Thursday that window has expired
SO you would then need to refer to post#9 if you do want to see the correct equation and my explanation behind it

If you do know of a way through which I can edit the original post, please do tell me

 

[Steve4Physics]

Oh I get you now
Coefficient of static friction- when body is at rest ( just rest)
Coefficient of limiting static friction - when body is just about to slide

No! The 'coefficient of static friction' and the 'coefficient of limiting static friction' are different names for same thing! The word 'limiting' is sometimes omitted simply for brevity.

For example, a block weighs 100N and is stationary on horizontal surface with μₛ=0.6. The limiting frictional force is 60N.

That means the frictional force can be any value up to 60N. E.g. if you apply a horizontal force of 53N (left) to the block, there will be a frictional force of 53N (right), so the block won’t move. There is no coefficient of friction associated with the value 53N.

 

[ShaunPereira]

No! The 'coefficient of static friction' and the 'coefficient of limiting static friction' are different names for same thing! The word 'limiting' is sometimes omitted simply for brevity.

For example, a block weighs 100N and is stationary on horizontal surface with μₛ=0.6. The limiting frictional force is 60N.

That means the frictional force can be any value up to 60N. E.g. if you apply a horizontal force of 53N (left) to the block, there will be a frictional force of 53N (right), so the block won’t move. There is no coefficient of friction associated with the value 53N.

Well that is exactly what I was taught in school. The attempt at brevity was the very thing that confused me into thinking that the both were two different things. Unfortunately there is no way I can edit post#6 where I have made that mistake but consider it understood and the mistake rectified.

So to conclude, is there anything wrong about post#9 where I have not made the incorrect distinction between limiting static friction and static friction. If there is please do tell me about it as i still have the option to edit that post while the posts I have made 24 hours ago do not have that option

 

[Steve4Physics]

So to conclude, is there anything wrong about post#9 where I have not made the incorrect distinction between limiting static friction and static friction. If there is please do tell me about it as i still have the option to edit that post while the posts I have made 24 hours ago do not have that option

I assume you are asking if your Post #9 equation:
"-kx (+/-) zmgcosΘ +mgsinΘ =0"
is OK.

The answer is: almost – but you haven’t made clear how the + and – signs apply. If I were writing it, I would have separate equations for ‘about to slide downhill’ and ‘about to slide uphill’.

 

[ShaunPereira]

I assume you are asking if your Post #9 equation:
"-kx (+/-) zmgcosΘ +mgsinΘ =0"
is OK.

The answer is: almost – but you haven’t made clear how the + and – signs apply. If I were writing it, I would have separate equations for ‘about to slide downhill’ and ‘about to slide uphill’.

Hmmmm... I thought I did, maybe not necessarily through two separate equations.
So here they are :
-kx +zmgcosΘ +mgsinΘ =0 for when the block is about to slide uphill
-kx -zmgcosΘ + mgsinΘ =0 for when the block is about to slide downhill

where z= coefficient of static friction

Is this correct now?

 

[Steve4Physics]

Hmmmm... I thought I did, maybe not necessarily through two separate equations.
So here they are :
-kx +zmgcosΘ +mgsinΘ =0 for when the block is about to slide uphill
-kx -zmgcosΘ + mgsinΘ =0 for when the block is about to slide downhill

where z= coefficient of static friction

Is this correct now?

Yes. Well done!
You could use one equation with +/- as long as you state that '+' applies when block is about to slide uphill and '-' applies for downhill. It's just a matter of personal preference. The important point is that there should be no ambiguity.

 

[ShaunPereira]

Yes. Well done!
You could use one equation with +/- as long as you state that '+' applies when block is about to slide uphill and '-' applies for downhill. It's just a matter of personal preference. The important point is that there should be no ambiguity.

HA Finally!

 

[ShaunPereira]

Thank you very much