Problem on Differential Pulleys

  • Thread starter nirmalya1basu
  • Start date
  • Tags
    Physics
In summary, "Problem on Differential Pulleys" discusses the mechanics and calculations involved in using differential pulleys, which are systems that allow for lifting heavy loads with minimal effort. The problem typically involves analyzing forces, tensions, and the mechanical advantage provided by the pulley system. It emphasizes the importance of understanding the principles of equilibrium and the relationship between load and effort in practical applications.
  • #1
nirmalya1basu
7
2
Homework Statement
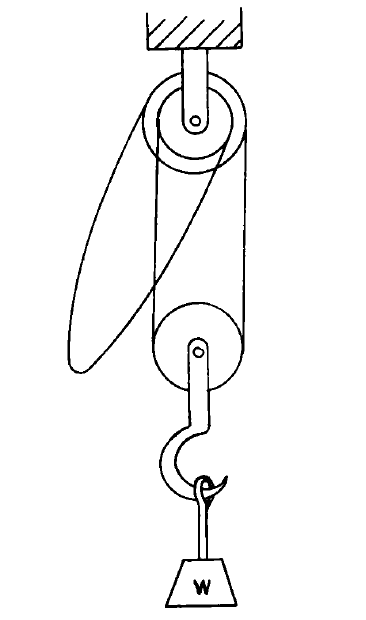
The differential pulley shown (vide the figure in the attached file) uses chain with N links per ft. The upper pulley has indentations which match the chain links, the larger sheave having n notches in its circumference and the smaller sheave, (n - 1) notches. (Each notch corresponds to two chain links.) The friction in the system is such that the ratio of the forces needed to raise or lower a weight W are in the ratio R. Assuming that the friction is the same in each direction, find the forces needed to raise W and to lower W.

Given answers:
Force needed to raise W = W*R / [n*(R - 1) + 1]
Force needed to lower W = W / [n*(R - 1) + 1]
Relevant Equations
1) Gravitational potential energy for one object = weight * height
2) Change in energy = force * (distance the force acts through)
3) Kinetic energy = (1/2)*m*(v^2)
4) Principle of conservation of energy
5) Principle of virtual work
Let the radius of the larger sheave in the upper pulley be r1, and the radius of the smaller sheave in this pulley be r2.
Given, the larger sheave has n notches in its circumference and the smaller sheave, (n - 1) notches.
Therefore, 2*pi*r1 corresponds to n notches, and 2*pi*r2 corresponds to (n - 1) notches.
Therefore, r1/r2 = n/(n - 1) ---> (1)
Also given, F(raising) / F(lowering) = R ---> (2)
Let, when the weight is raised or lowered, the upper pulley turns an angle x.
Then, the distance through which the weight displaces = (r1 - r2)*x = [{n/(n - 1)}*r2 - r2]*x = x/(n - 1).
After this, I have not been able to make further progress.
PhysicsForums_FigureForProblemOnDifferentialPulleys.png
 
Physics news on Phys.org
  • #2
You have not attempted to involve friction, but you know it is relevant.
 
  • Like
Likes MatinSAR
  • #3
Thank you, Sir, for your reply. I understand that friction is relevant, but, I am unable to write equations involving friction that will help in solving the problem. What I have thought is the following:

Work done by the lowering force = F(lowering) * {r2*x/(n - 1)}
Work done by the raising force = F(raising) * {r2*x/(n - 1)}
Work done by friction (in both lowering and raising) = F(friction) * {r2*x/(n - 1)}
Decrease in potential energy of the weight when lowered = W * {r2*x/(n - 1)}
Increase in potential energy of the weight when raised = W * {r2*x/(n - 1)}
Also given, F(raising) / F(lowering) = R

But, I am unable to proceed further. Please help me solve the problem.
 
  • #4
nirmalya1basu said:
Thank you, Sir, for your reply. I understand that friction is relevant, but, I am unable to write equations involving friction that will help in solving the problem. What I have thought is the following:

Work done by the lowering force = F(lowering) * {r2*x/(n - 1)}
Work done by the raising force = F(raising) * {r2*x/(n - 1)}
Work done by friction (in both lowering and raising) = F(friction) * {r2*x/(n - 1)}
Decrease in potential energy of the weight when lowered = W * {r2*x/(n - 1)}
Increase in potential energy of the weight when raised = W * {r2*x/(n - 1)}
Also given, F(raising) / F(lowering) = R

But, I am unable to proceed further. Please help me solve the problem.
You need to relate the work done by the user to the useful work done. If the weight is raised distance y, what is the useful work done? How does that relate to the friction and the actual work done by the user?
 
  • #5
It appears to me that if the weight is raised a distance y, then
the useful work done = W*y
Actual work done by the user = F(raising) * y
Work done by friction = F(friction) * y
Now, if we say that
Useful work done = Actual work done by the user - Work done by friction,
then we have
W*y = F(raising) * y - F(friction) * y
Then, dividing the LHS and the RHS of the equation by y, we have
W = F(raising) - F(friction)
But, this does not appear to me to be correct because that would mean that the resultant force acting on the weight W is 0, and so, the weight W is supposed to be at rest; but then, it could not be raised at all.
Could you please give me some suggestion regarding this?
 
  • #6
nirmalya1basu said:
... Actual work done by the user = F(raising) * y
This seems not to be correct.
The mechanical advantage of the device makes the magnitude of the hand force to be less than W and the length of pulled chain to be greater than y.
That manual work should be equal to the needed work to overcome internal friction plus W times y.

"The friction in the system is such that the ratio of the forces needed to raise or lower a weight W are in the ratio R."
This statement seems to imply that Manual F times R = W.

"Assuming that the friction is the same in each direction, find the forces needed to raise W and to lower W."
This statement seems to imply that gravity will be helping the hand when lowering the load.
 
  • #7
nirmalya1basu said:
this does not appear to me to be correct because that would mean that the resultant force acting on the weight W is 0
While there does need to be a net force to make the weight start moving, it does not need to move very quickly. So it can just be quite a small net force for a short time. Likewise, when the weight is nearly up to where the user is trying to move it to, the net force can be allowed to go negative; the weight slows to a stop at the desired height.
So it is quite ok to treat it as though there is no net force.
 
  • #8
Lnewqban said:
This seems not to be correct.
The mechanical advantage of the device makes the magnitude of the hand force to be less than W and the length of pulled chain to be greater than y.
That manual work should be equal to the needed work to overcome internal friction plus W times y.

"The friction in the system is such that the ratio of the forces needed to raise or lower a weight W are in the ratio R."
This statement seems to imply that Manual F times R = W.

"Assuming that the friction is the same in each direction, find the forces needed to raise W and to lower W."
This statement seems to imply that gravity will be helping the hand when lowering the load.
Sir, it does not appear to me that Manual F times R = W because the following answers to the problem are given:
Force needed to raise W = W*R / [n*(R - 1) + 1]
Force needed to lower W = W / [n*(R - 1) + 1]
 
  • #9
haruspex said:
While there does need to be a net force to make the weight start moving, it does not need to move very quickly. So it can just be quite a small net force for a short time. Likewise, when the weight is nearly up to where the user is trying to move it to, the net force can be allowed to go negative; the weight slows to a stop at the desired height.
So it is quite ok to treat it as though there is no net force.
Sir, I have understood your point. I will try to solve the problem using this concept.
 
  • #10
I have tried to solve the problem in the following way.
When the weight W is raised a distance y, then
Useful work done = Actual work done by the user - Work done by friction
Therefore, W*y = F(raising) * y - F(friction) * y
or, W = F(raising) - F(friction)
or, F(raising) - F(friction) = W ---> (1)

When the weight W is lowered a distance y, then
the lowering force and the gravitational force do work to overcome friction.
Therefore, work done by lowering force + work done by gravitational force = work done by friction
or, F(lowering) * y + W*y = F(friction) * y
or, F(lowering) + W = F(friction) ---> (2)

Also given,
F(raising) / F(lowering) = R ---> (3)

Now, solving equations (1), (2) and (3), we get
F(lowering) = 2*W/(R - 1)
F(raising) = 2*R*W/(R - 1)

But, these do not match the answers that have been given which answers are as follows:
F(raising) = W*R / [n*(R - 1) + 1]
F(lowering) = W / [n*(R - 1) + 1]

Could you please suggest what needs to be done?
 
  • #11
nirmalya1basu said:
I have tried to solve the problem in the following way.
When the weight W is raised a distance y, then
Useful work done = Actual work done by the user - Work done by friction
Therefore, W*y = F(raising) * y - F(friction) * y
or, W = F(raising) - F(friction)
or, F(raising) - F(friction) = W ---> (1)

When the weight W is lowered a distance y, then
the lowering force and the gravitational force do work to overcome friction.
Therefore, work done by lowering force + work done by gravitational force = work done by friction
or, F(lowering) * y + W*y = F(friction) * y
or, F(lowering) + W = F(friction) ---> (2)

Also given,
F(raising) / F(lowering) = R ---> (3)

Now, solving equations (1), (2) and (3), we get
F(lowering) = 2*W/(R - 1)
F(raising) = 2*R*W/(R - 1)

But, these do not match the answers that have been given which answers are as follows:
F(raising) = W*R / [n*(R - 1) + 1]
F(lowering) = W / [n*(R - 1) + 1]

Could you please suggest what needs to be done?
If the user pulls the rope down a distance ##y##, how far is weight raised?
 
  • #12
I have solved the problem in the following way.
When the weight W is raised a distance y, F(raising) acts through a distance [{2*r1/(r1 - r2)} * y], and F(friction) acts on the chain through a distance [{2*(r1 + r2)/(r1 - r2)} * y].
Then, we have
F(raising) * [{2*r1/(r1 - r2)} * y] - F(friction) * [{2*(r1 + r2)/(r1 - r2)} * y] = W*y
or, F(raising) * {2*r1/(r1 - r2)} - F(friction) * {2*(r1 + r2)/(r1 - r2)} = W ---> (1)

When the weight W is lowered a distance y, F(lowering) acts through a distance [{2*r2/(r1 - r2)} * y], and F(friction) acts on the chain through a distance [{2*(r1 + r2)/(r1 - r2)} * y].
Then, we have
F(lowering) * [{2*r2/(r1 - r2)} * y] + W*y = F(friction) * [{2*(r1 + r2)/(r1 - r2)} * y]
or, F(lowering) * {2*r2/(r1 - r2)} + W = F(friction) * {2*(r1 + r2)/(r1 - r2)} ---> (2)

We also have
r1/r2 = n/(n - 1) ---> (3)
F(raising) / F(lowering) = R ---> (4)

Solving equations (1), (2), (3) and (4), we get
F(lowering) = W/[n*R - (n - 1)]
F(raising) = W*R/[n*R - (n - 1)]

or
F(lowering) = W/[n*(R - 1) + 1)]
F(raising) = W*R/[n*(R - 1) + 1)]

Thank you, all of you, for the guidance that you have given me in solving this problem.
 
  • Like
Likes Lnewqban

FAQ: Problem on Differential Pulleys

What is a differential pulley and how does it work?

A differential pulley, also known as a chain hoist or differential chain block, is a mechanical lifting device that uses a combination of pulleys and a chain to lift heavy loads with minimal effort. It works on the principle of mechanical advantage, where the input force is multiplied to lift heavier loads. The differential aspect comes from the different sizes of the pulleys, which create varying degrees of mechanical advantage as the load is lifted.

What is the mechanical advantage of a differential pulley system?

The mechanical advantage (MA) of a differential pulley system is determined by the ratio of the diameters of the large and small pulleys. If D is the diameter of the larger pulley and d is the diameter of the smaller pulley, the mechanical advantage is given by the formula MA = D / (D - d). This means that the larger the difference between the pulley sizes, the greater the mechanical advantage and the easier it is to lift the load.

How do you calculate the load capacity of a differential pulley?

The load capacity of a differential pulley depends on the strength of the materials used in the chain and pulleys, as well as the mechanical advantage of the system. To calculate the load capacity, you need to consider the maximum load that the chain can safely support, the mechanical advantage provided by the pulley sizes, and any safety factors recommended by the manufacturer. It's essential to refer to the manufacturer's specifications and guidelines to ensure safe operation.

What are the common applications of differential pulleys?

Differential pulleys are commonly used in various industrial and construction settings where heavy loads need to be lifted and moved with precision and minimal effort. Applications include lifting machinery parts, construction materials, and other heavy objects in factories, workshops, shipyards, and warehouses. They are also used in automotive repair shops for lifting engines and other heavy components.

What are the safety considerations when using a differential pulley?

When using a differential pulley, it's crucial to follow safety guidelines to prevent accidents and equipment damage. Key safety considerations include ensuring the pulley and chain are in good condition and free of defects, not exceeding the rated load capacity, securing the load properly, and operating the pulley system smoothly without sudden jerks. Additionally, users should wear appropriate personal protective equipment (PPE) such as gloves and safety glasses, and ensure the working area is clear of obstructions and personnel who are not involved in the lifting operation.

Similar threads

Calculating the force for a differential pulley
Replies
20
Views
4K
Problem about a rigid body pulled by a mass
Replies
12
Views
2K
Springs and Pulleys - Force analysis
Replies
18
Views
478
Platinum resistance thermometer and Kirchoff's Laws
Replies
1
Views
2K
Force Between 2 Coaxial Current-Carrying Loops
Replies
4
Views
469
System of two pulleys and three masses
Replies
22
Views
4K
Time period of SHM & Energy conservation in pulley-spring-block system
Replies
24
Views
2K
Physics 3: Images, Interference and Difraction
Replies
1
Views
1K
(I.E. Irodov problem 1.72) Dynamics problem involving a pulley
Replies
28
Views
3K
How Do Sign Conventions Affect Focal Length Calculations?
Replies
8
Views
2K

Hot Threads

Recent Insights

Back
Top