Problem regarding understanding entropy

[mohamed_a]

I was reading about thermodynamics postulates when i came over the differnetial fundamental equation:

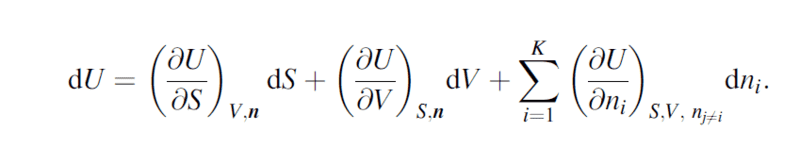
I understand that the second element is just pressure and last element is chemical energy, but he problem is i don't understand what is the use of entropy and how does it contribute to a systems energy
For example, if i have a container of gas and decided to increase entropy i will just pump out some gas and so the entropy will be increased as less molecules will have more space to move to, but isn't this just equivalent to the change in number of chemical energies (molecules) that exited and change in pressure.
Another example: if i try to exclude the last two elements and imagine how could I increase the energy of a system without changing pressure and chemical energy i am just left with temperature. but if i change the temperature, i would increase pressure and energy of the chemical substituents so why would i need to add a third element(entropy) if i could describe the system wit two only

I think entropy is the measure of inverse the intermolecular energy (hydrogen bonds,etc) , pressure is the measure of extramolecular energy (that is generated by breaking the intermolecular constraints) and chemical energy is the enthalpy of compounds (intramolecular energy). Am I right in my analysis? (i,e that kinetic energy of compounds and elements isn't considered in the third term but rather is included in the entropy)

And if this is correct why isn't nuclear energy added to the system ($E=mc^2$) as a forth element (intramolecular intranuclear energy)

 

[anuttarasammyak]

Say gas molecules are contained in a solid cylinder, dV=0, with no inlet/outlet, dn=0, the equation says
$$dU=\frac{\partial U}{\partial S}dS=TdS$$
We know high temperature gas has high internal energy and low temperature gas has low internal energy. Your question would be reduced to what temperature is and its relation to energy and entropy, or to the first principle of thermodynamics.
During process we usually consider, there is no change in mass energy mc^2 so its contribution to dU is zero. If we are dealing with nuclear reaction in reactor, we should take it into our thermodynamics.

 

[mohamed_a]

Say gas molecules are contained in a solid cylinder, dV=0, with no inlet/outlet, dn=0, the equation says
$$dU=\frac{\partial U}{\partial S}dS=TdS$$
We know high temperature gas has high internal energy and low temperature gas has low internal energy. Your question would be reduced to what temperature is and its relation to energy and entropy, or to the first principle of thermodynamics.
During process we usually consider, there is no change in mass energy mc^2 so its contribution to dU is zero. If we are dealing with nuclear reaction in reactor, we should take it into our thermodynamics.

in your approach why would i need temperature when i could just use pressure difference as a scale of internal energy you said no change in volume and no change in chemical substituents but there is a change of pressure. If i defined temperature to be the average kinetic energy , so simply increasing temperature would increase the kinetic energy and therefore increase the force acted on unit area by similar amount. What's the motivation to define a state function entropy

NB: just to be more clear, how could the possible number of microstates a system can exist in contribute to its energy how could i increase the number of microstates a system can exist in and expect its energy to change?

 

[anuttarasammyak]

Why don't you revisit the first principle of thermodynamics
$$dU=dQ-pdV=TdS-pdV$$
in your text ? Entropy and temperature are introduced there. This principle holds in general for the system where total energy is distributed to many small parts.