Problem related to a parallel plate capacitor

[PhysicsTest]

Homework Statement

a. The distance between the plates of a plane-parallel capacitor is 1cm. An electron starts at rest at the negative plate. If a direct voltage of 1000 V is applied, how long will it take the electron to reach the positive plate?
b. What is the magnitude of force which is exerted on the electron at the beginning and at the end of its path?
c. What is the final velocity?
d. If a 60-Hz sinusoidal voltage of peak value 1000 V is applied, how long will the time of transit be? Assume that the electron is released with zero velocity at the instant of time when the applied voltage is passing through zero.

Relevant Equations

F = qE, W = PE + KE

The diagram would look like this.

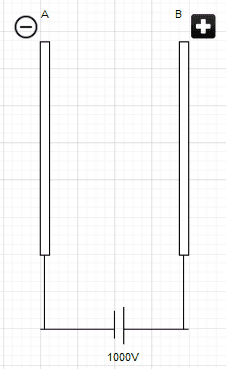
a. The total energy is conserved,
$KE_A + PE_A = KE_B + PE_B$
$KE_A=0; PE_A =1000$
$1000 = \frac{m v^2} {2}$
$2000 = {9.1}*10^{-31}*v^2$
$v^2 = \frac{2000 * 10^{31}} {9.1}; v = 46.8 * 10^{15}$
$v = at; = \frac {qVt} {md} ; t = \frac{vmd} {qV} seconds$
$t = 2.66 sec$
b. $F =q*E = \frac {qV} d = \frac{1.6*10^{-19} * 1000} {0.01} = 1.6 * 10^{-14} N$
c. $v =46.8 * 10^15 m/s$
d. This is a tougher one, one of the hints provided is expanding the sine function into power series
$\sin(\theta) = \theta - \frac{{\theta}^3} 6$
The sine function is $1000\sin(120\pi t)$
$V = 1000\sin(120\pi t) - 1000^3\frac {{\sin^3(120\pi t)}} 6$
$ma = qE; ma = \frac{qV} {d}; \frac {mv} t = \frac{qV} {d}$
$v =\sqrt{\frac{2qV} m}$
Substituting v, i get t. Is the approach correct?

 

[haruspex]

$KE_A=0; PE_A =1000$

A potential energy (something you might measure in J) cannot be equal to an electric potential (which you may measure in Volts).

 

[PhysicsTest]

Sorry my mistake it is $U = qV$

 

[haruspex]

Sorry my mistake it is $U = qV$

Right. So how does that change your answers?

 

[PhysicsTest]

The total energy is conserved,
$KE_A + PE_A = KE_B + PE_B$
$KE_A=0; PE_A =1.6*10^{-19} * 1000$
$1.6*10^{-16} = \frac{m v^2} {2}$
$3.2*10^{-16} = {9.1}*10^{-31}*v^2$
$v^2 = \frac{3.2 * 10^{15}} {9.1}; v^2 = 3.5 * 10^{14}; v = 1.875 * 10^7 m/s$
$v = at; = \frac {qVt} {md} ; t = \frac{vmd} {qV} seconds$
$t = 1.06 nsec$
b. $F =q*E = \frac {qV} d = \frac{1.6*10^{-19} * 1000} {0.01} = 1.6 * 10^{-14} N$
c. $v =1.875 * 10^7 m/s$
d. This is a tougher one, one of the hints provided is expanding the sine function into power series
$\sin(\theta) = \theta - \frac{{\theta}^3} 6$
The sine function is $1000\sin(120\pi t)$
$V = 1000\sin(120\pi t) - 1000^3\frac {{\sin^3(120\pi t)}} 6$
$ma = qE; ma = \frac{qV} {d}; \frac {mv} t = \frac{qV} {d}$
$v =\sqrt{\frac{2qV} m}$
Substituting v, i get t. Is the approach correct?

 

[PhysicsTest]

So for part d, can i assume that the electron will be oscillating between the two plates as the voltage is sinusoidal for positive values of sine value in one direction and for negative values in the other direction?

 

[haruspex]

$V = 1000\sin(120\pi t) - 1000^3\frac {{\sin^3(120\pi t)}} 6$

You want a power series in theta, not in sin(theta).
But you already know the answer is of the order of 100s of nsec. In such a short time sine is effectively a straight line.

$ma = \frac{qV} {d}; \frac {mv} t = \frac{qV} {d}$

Don't confuse instantaneous acceleration (a) with average acceleration (v/t).

 

[Delta2]

In such a short time sine is effectively a straight line.

You mean this $\sin120\pi t$ which is very low frequency(60hz frequency, relatively "big" period 17ms=17Million ns) hence it doesn't change a lot within 100ns..

 

[Steve4Physics]

Substituting v, i get t. Is the approach correct?

Haruspex has directed you well but if I may, I’d like to add a few points.

In your first attempt, you calculated the electron travels much faster than the speed of light but still took over 2s to travel 1cm! That should have signalled that you had made some serious mistake(s) and helped you find them.

The values supplied have a precision of only 1 significant figure. So it makes no sense to give a final answer like $v = 1.875*10^7 m/s$. Round to 1 or 2 sig. figs. I’d go for 2 significant figures here. (But use unrounded values in calculations to minimise cumulative rounding errors.)

Remember average velocity is half the final velocity (if starting from rest and having constant acceleration). So you could have found the time more simply:
$time= \frac{displacement}{average-velocity} = \frac{0.01}{0.5 *1.875*10^7} = 1.1*10^-9s$

You should be familiar with the small angle approximation which tells you sin(θ) ≈ θ if θ (in radians) is small. ‘θ’ is simply the first term in the power-series expansion of sin(θ). So you know that if the transit time is much less than (T = 1/f =) 1/60 s, you can write:

V(t) = 1000sin(120πt) ≈ 1000(120πt) ≈ 377000t (for small values of t)

Acceleration is no longer constant so you can’t use the simple (constant acceleration) kinematics equations. You will need a little calculus I think.

Be accurate/consistent with symbols, so don’t mix ‘seconds’, ‘sec’ and ‘s’. The SI symbol for seconds is ‘s’. Similarly the symbol for the unit 'hertz' is ‘Hz’, not ‘hz’.

 

[PhysicsTest]

Thank you for the clarity. The modified equations for problem (d)
$\frac{mv^2} 2 = q * 377000t$
$ma = \frac{q*V(t)} d => ma = \frac{q*377000t} {0.01}$
$m \frac{dv} {dt} = q*377*10^5 t; mv = 377*10^5 q \int t dt$
$mv = 377*10^5*q*\frac {t^2} 2$
$m^2v^2 = 1.13*10^{-9} * t^2$
$m^2 v^2 = 1.27*10^{-18} * t^4$
$m*2*q*377*10^3 t = 1.27*10^{-18} *t^4$
$9.1*10^{-31}*1.69*10^{-19}*377*10^3 = 1.27*10^{-18} * t^3$
$t = 3.57ns$

 

[Steve4Physics]

Thank you for the clarity. The modified equations for problem (d)
$\frac{mv^2} 2 = q * 377000t$
$ma = \frac{q*V(t)} d => ma = \frac{q*377000t} {0.01}$
$m \frac{dv} {dt} = q*377*10^5 t; mv = 377*10^5 q \int t dt$
$mv = 377*10^5*q*\frac {t^2} 2$
$m^2v^2 = 1.13*10^{-9} * t^2$
$m^2 v^2 = 1.27*10^{-18} * t^4$
$m*2*q*377*10^3 t = 1.27*10^{-18} *t^4$
$9.1*10^{-31}*1.69*10^{-19}*377*10^3 = 1.27*10^{-18} * t^3$
$t = 3.57ns$

I can’t follow your working. Solutions using symbols (until the end) are often easier to read/follow. Here’s a bit more help than I should provide...

$V(t) = kt$ where $k = 3.77*10^5 V/s$
$$F = qE = \frac{qV}{d} = \frac{qkt}{d}$$Applying F = ma gives:$$\frac{qkt}{d}= m\frac{d^2x}{dt^2}$$$$\frac{d^2x}{dt^2} = \frac{qk}{md}t$$
Integrate twice and you get x as a function of t. Then set x=d and you’ll have an equation from which you can find t.

 

[haruspex]

You mean this $\sin120\pi t$ which is very low frequency(60hz frequency, relatively "big" period 17ms=17Million ns) hence it doesn't change a lot within 100ns..

No, I mean the slope doesn't change much.

 

[Delta2]

Thank you for the clarity. The modified equations for problem (d)
$\frac{mv^2} 2 = q * 377000t$
$ma = \frac{q*V(t)} d => ma = \frac{q*377000t} {0.01}$
$m \frac{dv} {dt} = q*377*10^5 t; mv = 377*10^5 q \int t dt$
$mv = 377*10^5*q*\frac {t^2} 2$
$m^2v^2 = 1.13*10^{-9} * t^2$
$m^2 v^2 = 1.27*10^{-18} * t^4$
$m*2*q*377*10^3 t = 1.27*10^{-18} *t^4$
$9.1*10^{-31}*1.69*10^{-19}*377*10^3 = 1.27*10^{-18} * t^3$
$t = 3.57ns$

The first equation doesn't hold , because conservation of mechanical energy doesn't hold when the potential energy is time varying. More on this shortly...

 

[Delta2]

No, I mean the slope doesn't change much.

Yes well the slope is $120\pi\cos120\pi t$ which doesn't change much with the same logic of post #8...

 

[haruspex]

Yes well the slope is $120\pi\cos120\pi t$ which doesn't change much with the same logic of post #8...

But sine changes much more than cosine in the vicinity of 0. If we take sine as not changing then the electron goes nowhere.

 

[Delta2]

But sine changes much more than cosine in the vicinity of 0. If we take sine as not changing then the electron goes nowhere.

Yes ok, you made me understand that the logic of post #8 is not sound because locally (at the vicinity of 0 for example) the function might be undergoing great changes.