Problem with setting the region of integration

  • Thread starter Amaelle
  • Start date
  • Tags
    Integration
In summary, the conversation is about a problem with the solution of some integrals. The speaker is confused about the choice of borders for the integral and questions why c is used as the upper limit instead of b/a. The other person explains that for the given domain, c is indeed greater than b/a and therefore, it can be used as the upper limit. They also mention that the area of integration is a triangle and that c is not actually used in the calculation. The speaker expresses their appreciation for the explanation.
  • #1
Amaelle
310
54
Homework Statement
look at the image below!
Relevant Equations
double integrals
Good day !
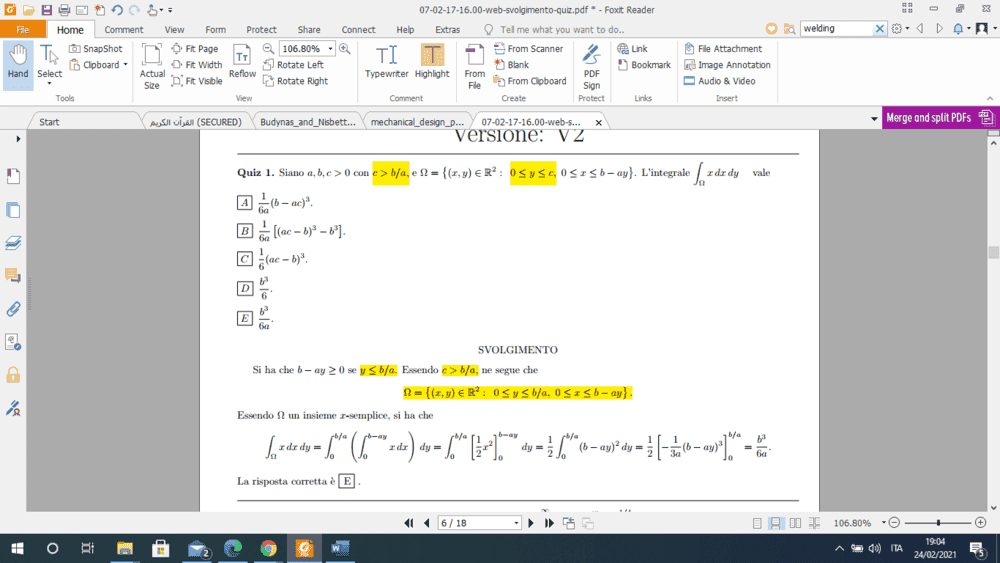
I have a problem with the solution of the floowing integrals
Indeed i don't understand why they choose such borders for integral
b/a<c
y<c
doesn't mean that y<b/a !
many thanks in advance!

1614189909864.png
 

Attachments

  • 1614189699163.png
    1614189699163.png
    37.4 KB · Views: 117
Physics news on Phys.org
  • #2
Amaelle said:
doesn't mean that y<b/a !
For ##(x,y)\in\Omega##, yes that is correct. That's why they can set the upper limit on the outer integral to ##b/a## rather than ##c##, even though ##c## may be greater than ##b/a##.

The area of integration is a triangle with vertices (0,0), (0, b/a), (b,0).

Given that c>b/a, the value of c is not used in the calculation. I think they just put it in the question to confuse people!
 
  • Love
Likes Amaelle
  • #3
that was an amzing shot! thanks a million!
 

FAQ: Problem with setting the region of integration

What is the "region of integration" in a scientific context?

The "region of integration" refers to the specific area or domain over which a mathematical or scientific function is being analyzed or evaluated. It can also refer to the boundaries or limits within which a particular phenomenon or process is being studied.

Why is setting the region of integration important in scientific research?

Setting the region of integration is important because it allows for a more precise and accurate analysis of a particular phenomenon or process. By defining the boundaries or limits of the region, scientists can control for extraneous variables and focus on the specific area of interest.

What are some common challenges or problems with setting the region of integration?

One common problem with setting the region of integration is determining the appropriate boundaries or limits. This can be particularly challenging when dealing with complex or multidimensional functions. Additionally, inaccuracies in defining the region can lead to errors in analysis and interpretation of results.

How can scientists ensure that the region of integration is accurately set?

To ensure the accuracy of the region of integration, scientists can use various techniques such as numerical methods, computer simulations, or physical experiments. It is also important for scientists to carefully consider the variables and parameters involved in the function and carefully define the boundaries or limits of the region.

Can the region of integration change in scientific research?

Yes, the region of integration can change in scientific research. As new data and information are gathered, scientists may need to adjust the boundaries or limits of the region in order to account for new variables or refine their analysis. This is a normal part of the scientific process and allows for a more comprehensive understanding of a phenomenon or process.

Similar threads

Problem with the region of an integral
Replies
2
Views
1K
Double Integral Problem: Incorrect Jacobian Calculation for Polar Coordinates
Replies
4
Views
1K
Calculate this Integral around the Circular Path using Green's Theorem
Replies
3
Views
1K
Problem integrating with the disk method
Replies
5
Views
1K
Question about a double integral region
Replies
5
Views
1K
Obtain a nonzero solution of ##y''-4y'+x^2(y'-4y)=0## by inspection
Replies
7
Views
1K
Solving non-homogeneous system of ODE using matrix exponential
Replies
4
Views
759
Double Integral via Appropriate Change of Variables
Replies
3
Views
1K
Need help deducing the region for this double integration problem
Replies
9
Views
1K
Where to use polar (cylindrical coor.) in double and triple integrals
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top