bearn
- 11
- 0
What are the step-by-step in solving these problems?
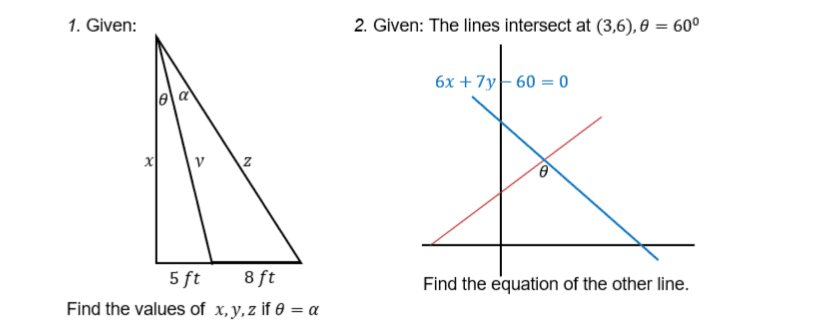
Country Boy said:For (1) I assume the lower left angle is a right angle.
Got it! Thank You so much!Country Boy said:For (2) the blue line is given by 6x+ 7y= 60 or y= -(6/7)x+ 60/7. Its slope is -6/7 so the "exterior angle" of that triangle is arctan(-6/7)= 139.4 degrees. The interior angle is 180- 139.4= 40.6 degrees. Since $\theta= 60$ degrees the third angle, where the red line crosses the base is 180- 60- 40.6= 120- 40.6= 79.4 degrees. So the slope of the red line is tan(79.4)= 5.34.
y= 5.34(x- x_0)+ y_0 where (x_0, y_0) is any point on the line. We are told that (3, 6) is such a point.