Problems with Landau Wang algorithm in fortran

[IreneFerri]

TL;DR Summary

Ask for help in a computational issue implementing the Landau-Wang algorithm on a magnetic spins model with Heisenberg hamiltonian.

I have been struggling for over a month now with a problem I cannot fix. I would really appreciate any comment or guidance. Thank you!

I am considering an Ising-like model with N agents that han hold one of the following 3 states, represented by vectors:

state + : vector (1 0)
state 0 : vector (0 alpha) ; alpha is a real, positive parameter
state - : vector (-1 0)

All agents are connected (fully connected graph)

The interaction hamiltonian is H = -J*sum(s_i*s_j), extended to all pairs (This is the Heisenberg hamiltonian, Ising-like).
The system's energy only depends on the number of agents in each state as follows:

E = 0.5*(((num(+) - num(-))**2) + alpha**2 * num(0) - num(+) - num(-) - alpha**2 * num(0))

I am determining a first order transition using the wang-landau algorithm but I have problems with the implementation. I get unvisited configurations, so the histogram never becomes flat.

I am trying with an arbitrary value of alpha = 0.2

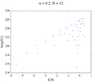
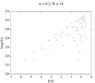
It seems to work for N <= 14 (I attach figures of the unnormalised logarithm of the density states array versus energy) but I doesn't work for bigger systems.

My code is public in github in the following link: https://github.com/IreneFerri/alpha3states.git

 

[Baluncore]

Welcome to PF.
Unfortunately I see no code to download when I follow the github link.
Only; readme.MD

 

[IreneFerri]

Hello, and thank you for your quick reply. I'm sorry for the confusion, I am super-begginer.
I think that now it is visible. I have entered the site without loggin and I am capable of seeing the code folder. Please, let me know if you can access the information now.

 

[Baluncore]

Please, let me know if you can access the information now.

Yes it is there. I will look at it later.

 

[Timo]

I didn't really look into your code specifically, yet. But I got a little interested in the question and started writing an own version. The first thing I wonder about is why you are approaching this model with a Monte-Carlo approach. The model seems simple enough to handle without. You already noted that the energy E(N+, N-, Na) only depends on the number of spins in the three possible states, which already is the key element that makes the model simple. The density of states can be derived as g(N+, N-, Na) = (N+ + N- + Na)! / (N+! N-! Na!). Unless you are trying to learn how WL sampling works, I don't see why you would use a slow computer algorithm to reproduce a simple combinatorics result.

I see no principal problems why WL should fail, though. And my current code version seems to run fine (tested up to N=50). I'll try some improvements I saw in your code (determining the possible energies up-front) and see if that leads to problems. I have been using an initial weight change of 1 (factor or e) and a flatness criterion that the bin with the least visits has at least 80% of the visits as the bin with the most visits, and that all bins have been visited at least 2000 times.

 

[Timo]

So I had a look at the code. I've never seen Fortran code before, but here's a few comments based on what I understood:

1. Most importantly, the line DO while ((ln_f > eps).and.(istep < MCtot)) seems to terminate the sampling when MCtot steps are reached. Your configuration file sets them at 10k steps. That is way too little for a proper sampling.
2. You seem to check the histogram of visits every N steps, where N is the number of spins. That's technically okay, but your code will spend most of its time checking your histogram. Do that every few thousand steps, instead (I check every 20k steps, I think).
3. I remember the flatness-check as min(H) >= tol * max(H). You seem to implement min(H) >= tol * mean(H). I think the tol*max(H) version is more robust on a theoretical level (it removes the possibility that one state has been visited extraordinarily often and causing the finer-grain loops to never reach it, anymore). Not sure if that matters in practice, though.
4. I don't feel well about your line do n1 = 0, int(N-n0)/2 . You probably want to abuse the symmetry of you Hamiltonian there. But the naming of your variables (n0, n1 and n_1) makes my head hurt and I cannot see if that really works (and if you properly take all rounding effects into account). Since you have an explicit cleanup stage to remove degenerate states later, I recommend to just run the loop over all possible states.
5. You seem to model each spin explicitly in your MC state. That is fine. But if you are a bit careful about your MC steps, it is sufficient to model the microstate as a tuple of three integers (N+, N-, Na). I originally thought that would make a lot of performance difference, but I am not sure anymore.
6. I am a bit worried about your checks for rounding errors, and if you shoot yourself in the foot with them (what happens when eps == alpha2 ?). If you have exactly one function E(N+, N-, Na) that takes integer numbers, and if you use that function exclusively to calculate energies, then you do not need these checks. Just mentioning that, though. For now, I recommend to leave the checks in.

 

[IreneFerri]

So I had a look at the code. I've never seen Fortran code before, but here's a few comments based on what I understood:

1. Most importantly, the line DO while ((ln_f > eps).and.(istep < MCtot)) seems to terminate the sampling when MCtot steps are reached. Your configuration file sets them at 10k steps. That is way too little for a proper sampling.
2. You seem to check the histogram of visits every N steps, where N is the number of spins. That's technically okay, but your code will spend most of its time checking your histogram. Do that every few thousand steps, instead (I check every 20k steps, I think).
3. I remember the flatness-check as min(H) >= tol * max(H). You seem to implement min(H) >= tol * mean(H). I think the tol*max(H) version is more robust on a theoretical level (it removes the possibility that one state has been visited extraordinarily often and causing the finer-grain loops to never reach it, anymore). Not sure if that matters in practice, though.
4. I don't feel well about your line do n1 = 0, int(N-n0)/2 . You probably want to abuse the symmetry of you Hamiltonian there. But the naming of your variables (n0, n1 and n_1) makes my head hurt and I cannot see if that really works (and if you properly take all rounding effects into account). Since you have an explicit cleanup stage to remove degenerate states later, I recommend to just run the loop over all possible states.
5. You seem to model each spin explicitly in your MC state. That is fine. But if you are a bit careful about your MC steps, it is sufficient to model the microstate as a tuple of three integers (N+, N-, Na). I originally thought that would make a lot of performance difference, but I am not sure anymore.
6. I am a bit worried about your checks for rounding errors, and if you shoot yourself in the foot with them (what happens when eps == alpha2 ?). If you have exactly one function E(N+, N-, Na) that takes integer numbers, and if you use that function exclusively to calculate energies, then you do not need these checks. Just mentioning that, though. For now, I recommend to leave the checks in.

Hello again:

First of all, thank you so much for your advice. It took a little bit to me to implement all your observations to my work, but I finally did it. However I'still struggling to find the right solution. I'm going to answer to your comments and then I will expose the problems I get now.

As you say, I don't need Wang-Landau sampling to calculate the density of states for the a fully connected network, in fact I want to apply it to other kind of networks, but I'm starting for the fully connected case because is the simplest, therefore I could gain some confidence on my code before. I have though written a small code in python which calculates the exact density of states so I can compare the results and be sure they are ok.

1. About the number of steps used to achieve the selected threshold for the modifier ln_f, you are right, is too low, just works this way for N=14, but I change it when I try to calculate higher sizes. The problem is that even with a huge number of steps the program fails for N>=16, there are unvisited configurations and the histogram does not become flat, not even once, yet for N=14 works just fine.

2. Same thing as before, I am aware that the checking should be done less frequently, I just adjust it in every run. And sometimes it is useful to me to set it to '1' because this way I can follow every step of the calculation printing on the screen. But you are right, it makes the code awfully slow.

3. It's good to know, however I just have checked it out and the problem persists.

4. I have followed your advice in the new code I have written, but I have not tried to changed it in the old one. However I have checked carefully that this wasn't the reason it failed using a program in python which compares the arrays obtained with the two methods and tests that they match (checked up to N=100).

5. This was also suggested by my professor so I ended up doing it. The second code is now visible in the github repository (https://github.com/IreneFerri/alpha3states.git) . It achieves flat histograms for any size N, however the results are wrong. I attach here a comparison of the output of my 3 programs: the exact calculation in python, the first Wang-Landau code we already spoke about, and the new program which uses the tuple (n1, n0, n_1) instead of the explicit spins array. The problem is described in detail in Github>issues, but it is easy to see that the results of the first code did match the exact solution, so maybe the problem for larger N was related to the rounding errors, as you suggested in the comment 6. This is not a problem anymore since I can find the index with an exact function.

6. Already explained in 5.

So, basically now I have the old code, which I know it works for N=14 but cannot perform calculations for bigger sizes, and a second code that achieve flat histograms for any size but delivers crazy results. I am stranded again, don't know what to try next.

Thank you for reading so carefully the code, I know I am super-newbie and it must be pretty hard to read, I tried to make it more clear this second time.

One last thing, I also attach here a table with the execution times for every program, just to remark that for N=14 the first code is faster than the second one. Not sure if that is true for larger N's.

 

[Fred Wright]

It occurs to me that you may have trouble with the random number generator in your code. Does it have a long enough period before the sequence repeats? This might explain why your code works for small $N$ but fails for large $N$.

 

[IreneFerri]

It occurs to me that you may have trouble with the random number generator in your code. Does it have a long enough period before the sequence repeats? This might explain why your code works for small $N$ but fails for large $N$.

Good point, I have no idea and it's the kind of thing it would never have occurred to me. I will dig in a bit and see if that's the issue, thank you!