Process Control (transfer function) problem

[guiromero]

TL;DR Summary: transfer function

Hello,

I have a doubt on this exercise from my post graduation course:
____________________________________________________________________________________________________
The transfer funtion of a series RL circuit is given by:

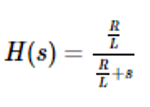
Determine the answer y(t) for an entry signal given by x(t) = u(t) V:

__________________________________________________________________________________________________

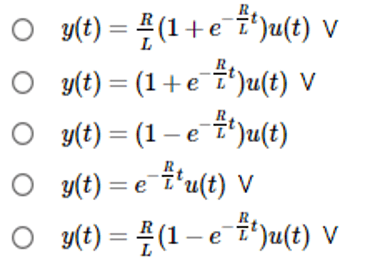
From the Laplace table, I find the closest association would be e^-at, for F(s) = 1/s+a. Then the answer would be "d", but I'm not sure if this association is correct, because F(s) is not exactly 1/s+a, it's more likely a/s+a, where a = R/L.

Could someone give me a clear answer?

Thanks a lot!

 

[FactChecker]

1) Use parentheses. If you mean 1/(s+a), then write 1/(s+a), not 1/s + a. Correct all those errors.
2) Define u(t).
3) Compare the y(t) values at $t=0$ and $t=\infty$ of the optional answers with what you would expect from a first order lag transformation, H(s). That should rule out practically all the wrong answers.