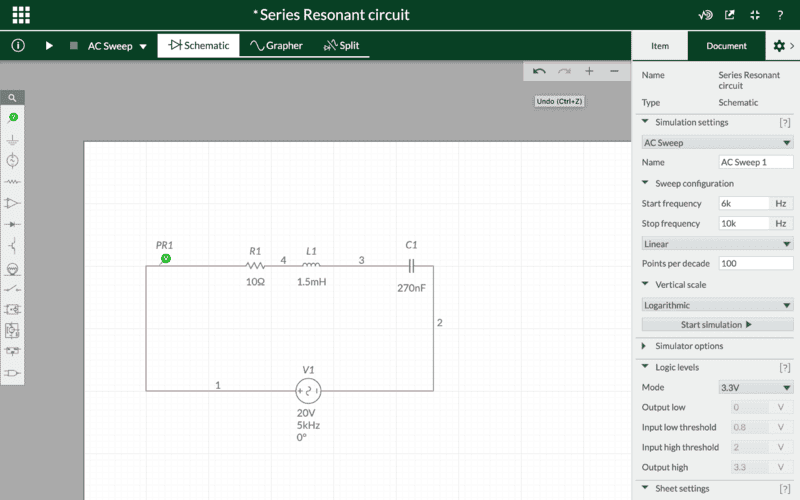
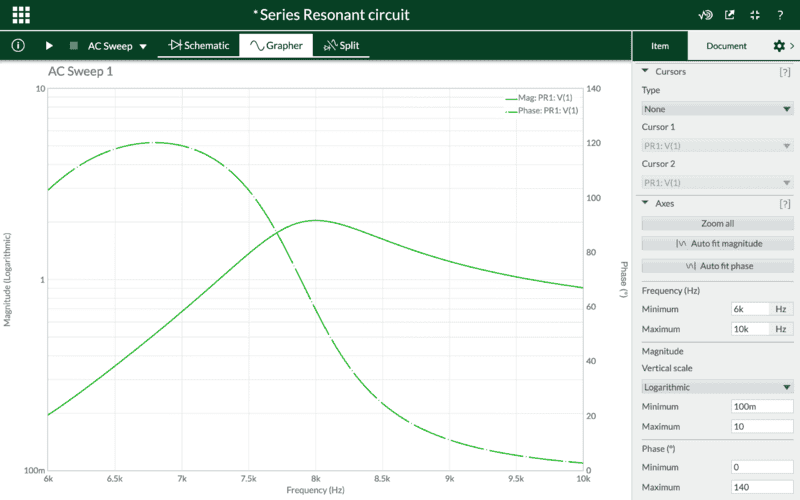
The discussion focuses on generating a resonance curve for a circuit between 6 kHz and 10 kHz, with participants addressing issues related to voltage measurement and circuit settings. There is confusion about the magnitude scale in the resonance plot, with suggestions that the current should peak at resonance according to the formula I = V1/R1, and that impedance should be considered. The phase of the plot appears correct, but the magnitude needs adjustment, particularly regarding the expected peaking at resonance. Participants recommend using LTSPICE for simulations, noting its popularity and effectiveness for basic circuits, while emphasizing that understanding concepts often comes from textbooks rather than simulators. Overall, the conversation highlights the importance of accurate measurements and understanding circuit behavior at resonance.