- #1
aatari
- 73
- 3
Hi Guys, could someone kindly look at my solutions and let me know if I did everything correctly.
Thanks a lot!
1. Homework Statement
A sniper fires a bullet at 120 m/s at 30° above the horizontal from the roof top of a 35 m high parking garage. If the bullet strikes the level ground beside the parking garage:
d = v.t
d = vt+1/2at^2
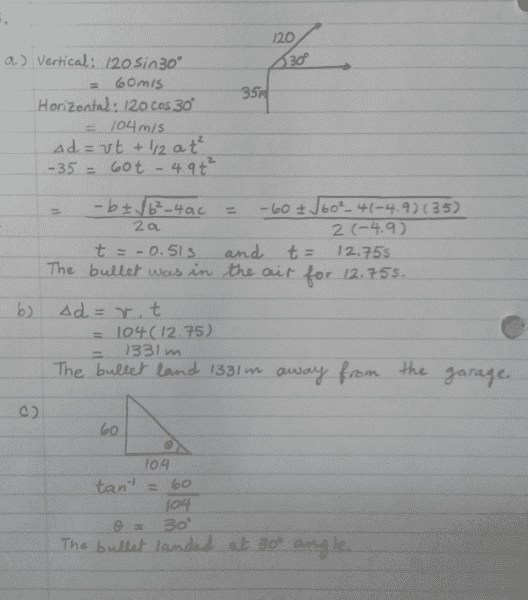 [/B]
[/B]
Thanks a lot!
1. Homework Statement
A sniper fires a bullet at 120 m/s at 30° above the horizontal from the roof top of a 35 m high parking garage. If the bullet strikes the level ground beside the parking garage:
- How long was the bullet in the air?
- How far from the base of the parking garage did the bullet land?
- At what angle did the bullet land?
Homework Equations
d = v.t
d = vt+1/2at^2