Proof by induction, puzzles by answer

[MegaDeth]

Ok, so there's this proof by induction question. I looked at the answer for it but I don't understand it.

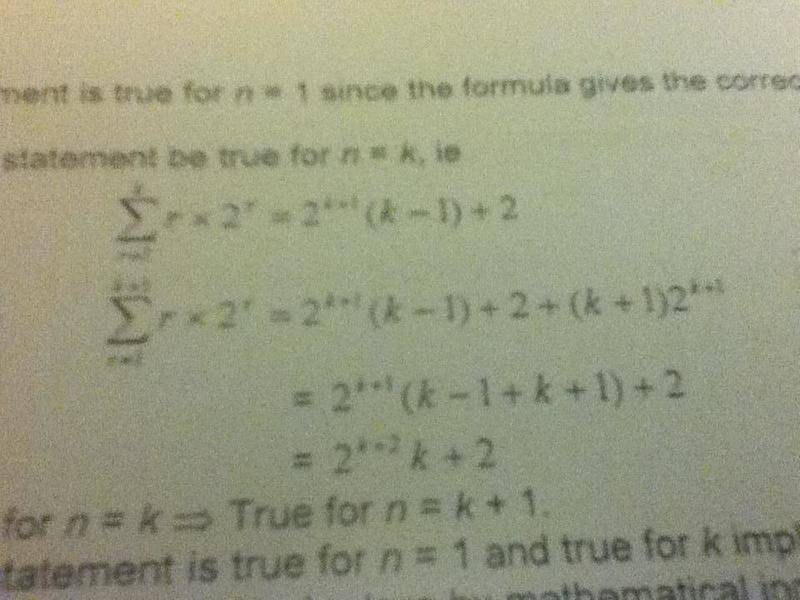
How does it get from being 2^(k+1) to being 2^(k+2)?

 

[Padfoot89]

You need to provide a little more background into your question, I think.

 

[HallsofIvy]

Your image did not link properly so it is impossible to answer your question.

 

[D H]

How does it get from being 2^(k+1) to being 2^(k+2)?

2^{k+1}(k-1+k+1) = 2^{k+1}(2k) = 2^{k+2}k

 

[rustynail]

you got [2^(k+1)](2k).

multiply 2^(k+1) by two, that is raising your exponent by 1. Hence 2^(k+2)