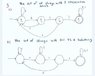
- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Proof Check Please: Mastering Two DFA's for Your Tutorial Questions
- Thread starter extatic
- Start date
-
- Tags
- Proof
In summary, a DFA, or deterministic finite automaton, is a mathematical model used to recognize patterns in a given input. Two DFA's can be compared to determine if they are equivalent, which can be useful in language recognition and software verification. To perform a proof check of two DFA's, a table is constructed and the states, input symbols, start state, and accept states are compared. The possible outcomes of a proof check are equivalent or not equivalent, which indicates if they accept the same language and have the same structure. Some practical applications of comparing two DFA's include software correctness, language equivalence, and DNA sequence analysis. It can also aid in designing efficient algorithms for language recognition and pattern matching.
Physics news on Phys.org
- #2
I like Serena
Homework Helper
MHB
- 16,336
- 258
Your first solution seems fine to me :)
In your second solution the string "01011" will fail when it shouldn't.
In your second solution the string "01011" will fail when it shouldn't.
- #3
extatic
- 6
- 0
you're right!
thank you mate
thank you mate
- #4
I like Serena
Homework Helper
MHB
- 16,336
- 258
extatic said:you're right!
thank you mate
You're welcome!
Oh, and welcome to PF. :)
- #5
- #6
I like Serena
Homework Helper
MHB
- 16,336
- 258
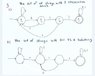
extatic said:Thank you :)
Hows this? better?
Perfect! :)
FAQ: Proof Check Please: Mastering Two DFA's for Your Tutorial Questions
What is a DFA?
A DFA, or deterministic finite automaton, is a mathematical model that is used to recognize patterns in a given input. It consists of a finite set of states, a set of input symbols, a transition function, a start state, and a set of accept states.
What is the purpose of comparing two DFA's?
The purpose of comparing two DFA's is to determine if they are equivalent, meaning that they accept the same language. This can be useful in various applications such as language recognition and software verification.
How do you perform a proof check of two DFA's?
To perform a proof check of two DFA's, you must first construct a table that shows the transition function for both DFA's. Then, you can check if the two DFA's have the same states, input symbols, start state, and accept states. Finally, you can compare the two tables to see if the transition function for each state and input symbol is the same.
What are the possible outcomes of a proof check of two DFA's?
The possible outcomes of a proof check of two DFA's are equivalent or not equivalent. If the two DFA's are equivalent, it means that they accept the same language and have the same structure. If they are not equivalent, it means that they accept different languages or have structural differences.
What are some practical applications of comparing two DFA's?
Comparing two DFA's can be used in various practical applications such as checking the correctness of software, verifying the equivalence of programming languages, and analyzing DNA sequences. It can also be useful in designing efficient algorithms for language recognition and pattern matching.
Similar threads
- Replies
- 1
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 0
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 10
- Views
- 488
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 3K
- Replies
- 16
- Views
- 3K
- Replies
- 6
- Views
- 3K
Share: