Proof derivative of a vector following precession motion

[Soren4]

I do not get some points of this proof about the time derivative of a unit vector $\hat{u}$ (costant magnitude) which is following a precession motion. The picture is the following.

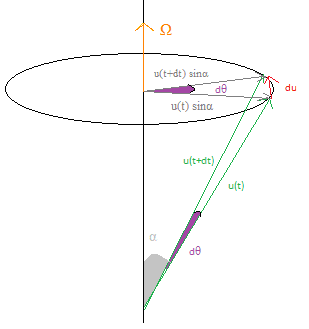
I want to prove that $$\frac{d\hat{u}}{dt}=\vec{\Omega}\wedge \hat{u}.$$

I'm ok with almost all the proof except the following points.

Consider the red vector d\hat{u}.
Since \hat{u} has constant magnitude,d\hat{u} must be orthogonal to \hat{u}.That's ok.

But why must d\hat{u} be orthogonal to \vec{\Omega} too (i.e. be tangential to a circle orthogonal to \vec{\Omega})?

Secondly how can I geometrically prove that the angle d\theta (the one in purple) that separates \hat{u}(t) and \hat{u}(t+dt) is the same that separates the projection of these two vectors on the circle orthogonal to \vec{\Omega} (the projections are \hat{u}(t) Sin(\alpha)and\hat{u}(t+dt) Sin(\alpha))?

 

[andrewkirk]

But why must d\hat{u} be orthogonal to \vec{\Omega} too (i.e. be tangential to a circle orthogonal to \vec{\Omega})?

Define $\vec v$ as the vector from the origin (the lowest point drawn on the diagram) to the centre of the drawn circle, and $\vec w(t),\vec w(t+dt)$ as the two vectors you have drawn from the centre of the circle to its circumference. Then we have $\vec u(t)=\vec v+\vec w(t)$, and $\vec u(t+dt)=\vec v+\vec w(t+dt)$.

A bit of geometry shows that the lengths of $\vec u(t)$ and $\vec u(t+dt)$ are the same. Let that length be $l$. Then $d\hat u=\hat u(t+dt)-\hat u(t)=\tfrac{1}{l}(\vec u(t+dt)-\vec u)=\tfrac{1}{l}(\vec w(t+dt)-\vec w)$. Both $\vec w(t+dt)$ and $\vec w$ are perpendicular to $\vec\Omega$, so their difference must be too, by the linearity of the dot product.