Proof of angle in path difference formula for two slits

[member 731016]

Homework Statement

Please see below

Relevant Equations

$r_2 - r_1 = d\sin\theta$

For this

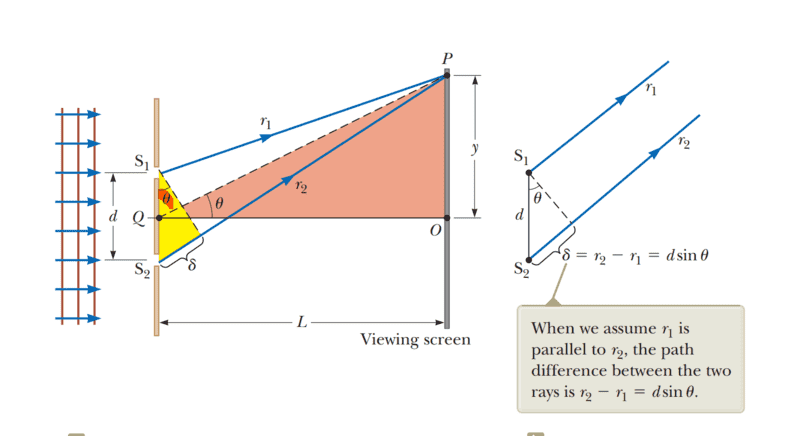
I am trying to prove that angle theta between PQ and QO is equal to theta highlighted so that I know I can use theta is the path difference formula. I assume that the rays $r_1$ and $r_2$ are parallel since $L >> d$

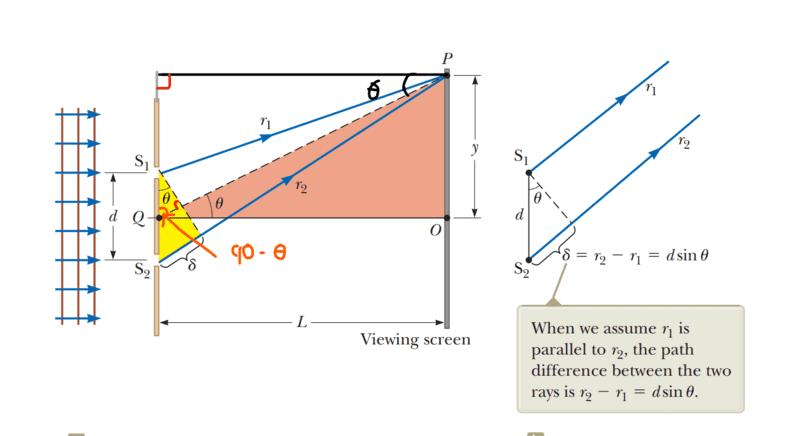
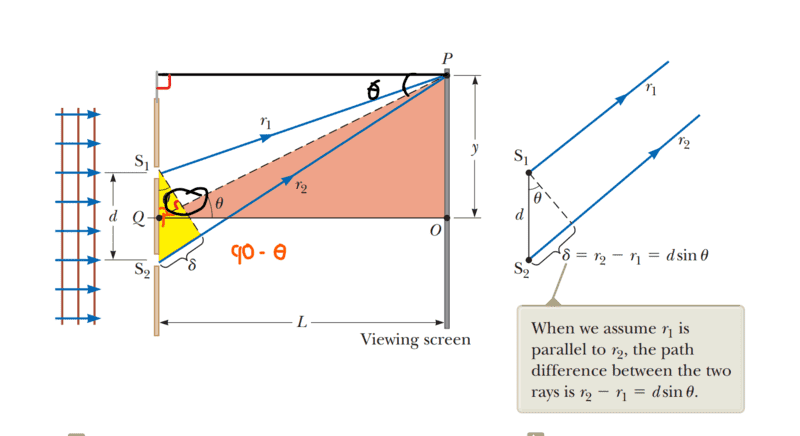
My proof gives that the two thetas are equal, however I am wondering whether my assumption that the right angle circled in black can be proved. Is there a way to prove this?

Many thanks!

 

[kuruman]

My proof gives that the two thetas are equal, however I am wondering whether my assumption that the right angle circled in black can be proved. Is there a way to prove this?

It's a right angle if you draw a line starting at S1 perpendicular to the ray from S2. That's not the point. The point is whether, when you draw this perpendicular, the segment labeled $\delta$ is the path length difference between the rays from S1 and S2. That is the case when the rays are nearly parallel.

 

[hutchphd]

You are free to choose that to be exactly a right angle before taking the limit that the screen is far away. Only in the limit are the distances delta and d easilly related to theta, but it can be shown that the approximation (not really an assumption) leads to errors that are very small in the Fraunhoffer (radiation) zone far from the slits.

 

[member 731016]

It's a right angle if you draw a line starting at S1 perpendicular to the ray from S2. That's not the point. The point is whether, when you draw this perpendicular, the segment labeled $\delta$ is the path length difference between the rays from S1 and S2. That is the case when the rays are nearly parallel.

Thank you for your reply @kuruman!

 

[member 731016]

You are free to choose that to be exactly a right angle before taking the limit that the screen is far away. Only in the limit are the distances delta and d easilly related to theta, but it can be shown that the approximation (not really an assumption) leads to errors that are very small in the Fraunhoffer (radiation) zone far from the slits.

Thank you for your reply @hutchphd !

True, I guess it is an approximation not assumption that $L >> d$. Sorry, what did you mean by errors very small in the Fraunhoffer zone?

Many thanks!

 

[hutchphd]

You can look up Fraunhoffer zone. It is really that the diffraction angles aren't too large and that the d<< L. So all the angles are small, and the results are simple. This approximation (Fraunhoffer) works for things other two slit diffraction

 

[jtbell]

Might get better results if you search on "Fraunhofer" instead of "Fraunhoffer", although Google is pretty good at catching "obvious" spelling errorz.

 

[member 731016]

You can look up Fraunhoffer zone. It is really that the diffraction angles aren't too large and that the d<< L. So all the angles are small, and the results are simple. This approximation (Fraunhoffer) works for things other two slit diffraction

Thank you for your help @hutchphd!

 

[member 731016]

Might get better results if you search on "Fraunhofer" instead of "Fraunhoffer", although Google is pretty good at catching "obvious" spelling errorz.

Thank you for your reply @jtbell!