- #1
eyehategod
- 82
- 0
I need help with proof. Can anyone lead me in the right direction?
http://i153.photobucket.com/albums/s208/nailbomb2/LastScan.jpg
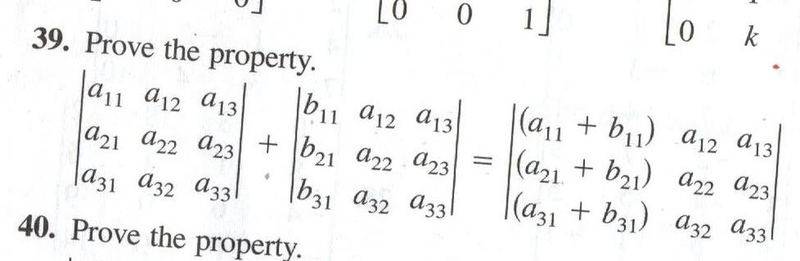
http://i153.photobucket.com/albums/s208/nailbomb2/LastScan.jpg
Attachments
Last edited: