mathlearn
- 331
- 0
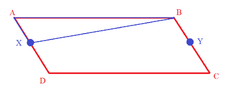
ABCD is a parallelogram . X is the midpoint of AD & Y is the midpoint of BC. Show that the area of $\triangle {ABX}$ is $\frac{1}{4}$ the area of ABCD
View attachment 6102
Can you help me with this proof ? were should i start ? I think It should be by proving
$\triangle{DBC} \cong \triangle{DBA} $ using SAS as DB is a common side DC= AB as ABCD is a parallelogram, $\angle {BDC} = \angle{DBA} $ alternate angles
And I can also predict that the use of midpoint theorem here
Many Thanks :)
View attachment 6102
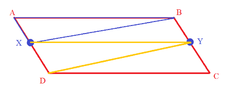
Can you help me with this proof ? were should i start ? I think It should be by proving
$\triangle{DBC} \cong \triangle{DBA} $ using SAS as DB is a common side DC= AB as ABCD is a parallelogram, $\angle {BDC} = \angle{DBA} $ alternate angles
And I can also predict that the use of midpoint theorem here
Many Thanks :)