Proof of Quotient Rule using Product Rule

[gomess]

Hey guys, just trying to understand how the quotient rule is derived, so I head over to wikipedia and saw this:

But I'm having some difficulty understanding what goes on between these two steps:

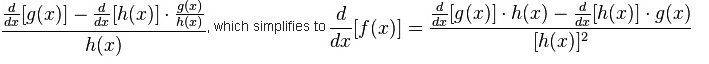
Could someone shed some light on this?

 

[STEMucator]

It looks like they are multiplying by $1 = \frac{h(x)}{h(x)}$

 

[gomess]

Oh, okay. Cant believe I didnt see that; it was so simple. Sorry to whoever moved my thread for posting in wrong the section. Thanks Zondrina!

 

[Mark44]

I moved it. This seemed more like a technical question than homework, so I move it here.

Also, what Zondrina said is exactly what happened - they multiplied by 1 in the form of h(x) over itself.

Also, if you post images again, crop or shrink them so that they fit. 900 pixels wide is about the maximum - yours is 1071 pixels wide, so causes the post to be too wide.

 

[gomess]

Alright, no problem. Thanks again guys.