Proof of the strong maximum principle

[mathmari]

Hey!

I am looking at the proof of the strong maximum principle:
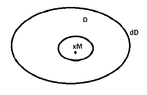
If a function $u$ satisfies the Laplace's equation at the open space $D$ and is continuous at the boundary $\partial{D}$ and achieves its maximum at $\partial{D}$ and at a point of $D$ then the function is a constant.

which is the following:

View attachment 2666

$x_M$ : the point where the function achieves its maximum

$x_M \in D$

$u(x) \leq u(x_M)=M, \forall x \in D$

$u(x)=u(x_M), \forall \text{ choice of circle }$

(Thinking)

I am facing some difficulties understanding this proof.. (Worried)

So, we take a circle with center $x_M$.

Then from the mean value property we have that:
$$u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds$$

We consider that $x_M \in D$ is the point at which $u$ achieves its maximum, so
$$u(x) \leq u(x_M)=M, \ \ \ \forall x \in D$$

So, we have the following:

$$M=u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds$$

But since the integral is at the boundary $\partial{D}$, and we have supposed that $M$ is the maximum of all points at $D$, we cannot say that
$$M=u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds \leq \frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{M}ds$$
right??

How can I continue then to show that the function is constant?? (Wondering)

 

[I like Serena]

Hey! (Mmm)

But since the integral is at the boundary $\partial{D}$, and we have supposed that $M$ is the maximum of all points at $D$, we cannot say that
$$M=u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds \leq \frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{M}ds$$
right??

Sure you can, but it doesn't help you. (Wasntme)

How can I continue then to show that the function is constant?? (Wondering)

Do something with Laplace's equation? (Thinking)

 

[mathmari]

Sure you can, but it doesn't help you. (Wasntme)

I thought I could it as followed:

$$M=u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds \leq \frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{M}ds = \frac{M}{2 \pi a} \int_{| \overrightarrow{r'}|=a}ds =M$$

So the symbol $\leq$ should be $=$, so $u=M$.

Is this wrong?? (Wondering)

Do something with Laplace's equation? (Thinking)

What could I do?? (Wondering)

 

[I like Serena]

I thought I could it as followed:

$$M=u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds \leq \frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{M}ds = \frac{M}{2 \pi a} \int_{| \overrightarrow{r'}|=a}ds =M$$

So the symbol $\leq$ should be $=$, so $u=M$.

Is this wrong?? (Wondering)

It is correct, but you are restating something you already know.
The left hand side is equivalent to the right hand side. (Wasntme)

What could I do?? (Wondering)

Well... you could for instance write down Laplace's equation in polar coordinates, separate the variables, add the boundary condition that the function of angle has period $2\pi$... (Wondering)

 

[mathmari]

Well... you could for instance write down Laplace's equation in polar coordinates, separate the variables, add the boundary condition that the function of angle has period $2\pi$... (Wondering)

$$u_{rr}+\frac{1}{r}u_r+\frac{1}{r^2}u_{\theta \theta}=0 ,\ \ \ 0 \leq \theta \leq 2 \pi, \ \ \ 0 \leq r \leq a$$

Applying the method of separation of variables, the solution is of the form $u(r, \theta)=R(r) \Theta(\theta)$

the boundary condition that the function of angle has period $2\pi$:
$u(a,\theta)=h(\theta), h(\theta)=h(2 \pi + \theta)$

The solution is the following:
$$u(r, \theta)=\sum_{n=0}^{\infty} [A_n \cos{(n \theta)}+B_n \sin{(n \theta)}]r^n \Rightarrow \dots \Rightarrow \\ u(r, \theta)=\frac{a^2-r^2}{2 \pi} \int_0^{2 \pi} \frac{h(\phi)}{a^2+r^2-2ar \cos{(\theta-\phi)}}d \phi$$

Do I have to use the last formula?? (Wondering)

 

[I like Serena]

$$u_{rr}+\frac{1}{r}u_r+\frac{1}{r^2}u_{\theta \theta}=0 ,\ \ \ 0 \leq \theta \leq 2 \pi, \ \ \ 0 \leq r \leq a$$

Applying the method of separation of variables, the solution is of the form $u(r, \theta)=R(r) \Theta(\theta)$

the boundary condition that the function of angle has period $2\pi$:
$u(a,\theta)=h(\theta), h(\theta)=h(2 \pi + \theta)$

The solution is the following:
$$u(r, \theta)=\sum_{n=0}^{\infty} [A_n \cos{(n \theta)}+B_n \sin{(n \theta)}]r^n \Rightarrow \dots \Rightarrow \\ u(r, \theta)=\frac{a^2-r^2}{2 \pi} \int_0^{2 \pi} \frac{h(\phi)}{a^2+r^2-2ar \cos{(\theta-\phi)}}d \phi$$

Do I have to use the last formula?? (Wondering)

Now that you mentioned it, didn't you have a proof (using that formula) that the average of the boundary is equal to u(0)?
Perhaps you can use that. (Thinking)

 

[mathmari]

Now that you mentioned it, didn't you have a proof (using that formula) that the average of the boundary is equal to u(0)?
Perhaps you can use that. (Thinking)

Yes, when we have a circle with center at $0$.

At the post #1, I took a circle with center at $x_M$, and then the average of the boundary is equal to
$$u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds$$

 

[mathmari]

Since $u$ achieves its maximum at $\partial{D}$ and at a point of $D$, do we maybe have to suppose that $M$ is the maximum of all points at $D$ and at $\partial{D}$?? (Wondering)

Then it would be as followed:

We take a circle with center $x_M$.

Then from the average of the boundary we have that:
$$u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds$$

We consider that $x_M \in \overline{D}$ is the point at which $u$ achieves its maximum, so
$$u(x) \leq u(x_M)=M, \ \ \ \forall x \in \overline{D}$$

($\overline{D}=D \cup \partial{D}$)

So, we have the following:

$$M=u(x_M)=\frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{u(\overrightarrow{r'})}ds \leq \frac{1}{2 \pi a} \int_{| \overrightarrow{r'}|=a}{M}ds$$

Can we continue from here?? (Worried)
Or should I use the average of the boundary in an other way?? (Thinking)

 

[I like Serena]

Since you can use the proposition that the value at the center is equal to the average at a circular boundary, it follows that all values at any circle around the center must be $M$... (Thinking)

 

[mathmari]

Since you can use the proposition that the value at the center is equal to the average at a circular boundary, it follows that all values at any circle around the center must be $M$... (Thinking)

I got stuck right now... (Worried)
Could you explain me further this implication?? (Thinking)

 

[I like Serena]

I got stuck right now... (Worried)
Could you explain me further this implication?? (Thinking)

I think it is like this.

Suppose we start with this point $x_M$ and draw a very small circle around it.
Since $x_M$ belongs to the interior of $D$, there must be a radius $r$ such that the circle fall entirely within $D$.

According to the Poisson kernel for the polar Laplace's equation, the value of $u$ at the center is the same as the average value of $u$ on a circle around that center.
Or isn't it? (Thinking)

So the values on our small circle should be sometimes lower than $u(x_M)$ and sometimes higher than $u(x_M)$ in such a way that the differences cancel out on average, giving an average of just $u(x_M)=M$.

However, since $M$ is actually the maximum on $D$, it follows that no value on the circle can be higher than $M$. And since the average has to come out as $M$, no value can be lower than $M$.
Therefore, each value on our small circle must have value $M$.
Or am I wrong? (Thinking)(Thinking)

 

[mathmari]

According to the Poisson kernel for the polar Laplace's equation, the value of $u$ at the center is the same as the average value of $u$ on a circle around that center.
Or isn't it? (Thinking)

Yes, it is like that! (Yes)

So the values on our small circle should be sometimes lower than $u(x_M)$ and sometimes higher than $u(x_M)$ in such a way that the differences cancel out on average, giving an average of just $u(x_M)=M$.

However, since $M$ is actually the maximum on $D$, it follows that no value on the circle can be higher than $M$. And since the average has to come out as $M$, no value can be lower than $M$.
Therefore, each value on our small circle must have value $M$.
Or am I wrong? (Thinking)(Thinking)

Ahaa... (Thinking) If there were values that are lower than $M$, would the average be lower than $M$??

 

[I like Serena]

Ahaa... (Thinking) If there were values that are lower than $M$, would the average be lower than $M$??

Any value lower than $M$ would pull the average down (assuming $u$ is continuous)... (Nod)

 

[mathmari]

Any value lower than $M$ would pull the average down (assuming $u$ is continuous)... (Nod)

Ahaa...Ok! I understand! Thank you very much! (Mmm)