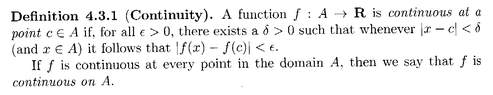Proof that Arcsin x is continuous ....

[Math Amateur]

Can someone please help me to prove that the function f(x) = Arcsin x is continuous on the interval [-1, 1] ...

Peter

 

[cbarker1]

What is the definition of continuous function in general?

 

[HallsofIvy]

An invertible function, y= f(x), is continuous at x= x_0 if and only if y= f^{-1}(x) is continuous at x= f(x_0).

 

[Math Amateur]

What is the definition of continuous function in general?

The definition of continuity in $$\mathbb{R}$$ is given in Stephen Abbott's book: Understanding Analysis, as follows:
View attachment 9348
Alternative characterizations of continuity are given by Abbott in Theorem 4.3.2 as follows:
View attachment 9349So to show (from first principles) that $$\text{Arcsin } x$$ is continuous on $$[-1, 1]$$ we would have to show that given an arbitrary point $$c \in [-1, 1]$$ that for every $$\epsilon \gt 0$$ we can find $$\delta \gt 0$$ such that

$$\mid x - c \mid \lt \delta \ \Longrightarrow \ \mid \text{Arcsin x } - \text{Arcsin } c \mid \lt \epsilon$$ ...But how do we proceed ... ?

Peter

- - - Updated - - -

An invertible function, y= f(x), is continuous at x= x_0 if and only if y= f^{-1}(x) is continuous at x= f(x_0).

Thanks for the help, HallsofIvy ...

Peter