Proof That The Following System Does Uniform Oscilations

[DorelXD]

Homework Statement

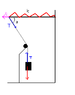
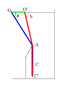
Well, we are given the following system, in which the rope, spring, and pulley is ideal. We know that for the angle a the system is in equilibrium. The question is, to show that if the angle a is small, the system does unfirom oscilations.

I don't know how to tackle this problem, it confuses me a little. We must show that the resultant force on the body is proportional to a constant and the displacement for the equilibrium position at a given time.

Homework Equations

Some basic trigonometry, with some tricks for aproximating the trigonometric function for small angles and basic vector addition, I think...

The Attempt at a Solution

Well, the first thing that is obvious is that if the system is at rest, then:

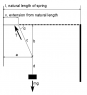
T\cos{a} = ky_0 , where y_0 is the initial comprimation of the spring, and k is its spring constant.

Writing the resultant force for the body we get that: R = T - mg. How do I continue from here? Can somebody help me, please :D ?

 

[haruspex]

You mean ".. if the deviations from angle a are small ...", right?
So consider a small deviation in a. Find how that affects the forces and accelerations, and thus how the deviation will change over time.

 

[DorelXD]

You mean ".. if the deviations from angle a are small ...", right?

Yes, indeed. :D

Well, the forces that act on the body are the tension and the weight. The tention depends on the amount of comprimation of the resort. I drew a picture. The resort compresses with OO'(green) and the body descends with CC'. I should find a relation between the two length. I drew the system in a more "gemoetrcal" way because we are interested in lengths, and relations between plain figures, right ?

Let us say that OO' = x because it seems a more familiar notation, and we are interested specifically in that length. When the system is in the state corespoding to the 'b' angle, the spring is compressed with: y_0 + x and we know the expression for y_0. So if the compression of the spring affects the tension, it affects the motion of the body, because tension acts on it. :D

Is my drawing and my judgement correct:D ? Tell me, please. If yes, how do we proceed? I haven't found a connection between CC' and OO'. :(

 

[voko]

OO' and AO' are related via the triangle OAO', where OA and angle O are constant. AO' + AC' = constant length of the rope.

Apart from this, I would use conservation of energy.

 

[DorelXD]

OO' and AO' are related via the triangle OAO', where OA and angle O are constant. AO' + AC' = constant length of the rope.

Apart from this, I would use conservation of energy.

Well there is no resitive force so the energy is conserved. Let us say that so CC' = d, because it's usefull. Also, in the initial position the potential energy of the body is 0 (for convenience).

E_a = E_b => \frac{ky_0^2}{2} = \frac{k(y_0 +x) ^2}{2} - mgd => mgd = \frac{k}{2}x(2y_0+x)

But, I don't see how that helps me. :D

 

[voko]

You are forgetting the kinetic energy.

 

[DorelXD]

You are forgetting the kinetic energy.

Right, sorry :D .

E_a = E_b => \frac{ky_0^2}{2} = \frac{k(y_0 +x) ^2}{2} - mgd + \frac{mv_x^2}{2}

where v_x is the speed corespoding to the elongation x.

Is it ok now? What's next? I haven't done the simplifications yet, but a first thing I notice is that I should connect v_x to x, somehow, right? And this isn't exactly straightforward because we don't have an uniform motion, the speed and acceleration are not constant.

And I wanted to thank you for answering me! So, what do we do next ? :D

 

[haruspex]

OO' and AO' are related via the triangle OAO', where OA and angle O are constant. AO' + AC' = constant length of the rope.

Apart from this, I would use conservation of energy.

I'm not sure that energy will make it easier. We don't need to solve the equations, just show that they approximate SHM.

DorelXD, what is the relationship between T and the force in the spring? Between x and force in the spring? Between x and the height of the mass? Between T and the acceleration of the mass? Put all that together.

 

[voko]

Right, sorry :D .

E_a = E_b => \frac{ky_0^2}{2} = \frac{k(y_0 +x) ^2}{2} - mgd + \frac{mv_x^2}{2}

where v_x is the speed corespoding to the elongation x.

The kinetic energy is in the motion of the mass, not in the motion of the ideal massless spring.

Is it ok now? What's next? I haven't done the simplifications yet, but a first thing I notice is that I should connect v_x to x, somehow, right? And this isn't exactly straightforward because we don't have an uniform motion, the speed and acceleration are not constant.

What you need to connect is $x$ and $d$. Then you can differentiate the energy equation, and you will obtain the second derivative of $d$ multiplied with the mass; whatever this is equal to is the force.

 

[DorelXD]

DorelXD, what is the relationship between T and the force in the spring?

Well, \frac{T}{cos{\alpha}} = k(y_0 + x )

Between x and force in the spring?

F_e = k(x+y_0)

Between x and the height of the mass?

That, I don't know. How can I find out ?

Between T and the acceleration of the mass? Put all that together.

Well I can find this out by writing Newton's second law, right? But I didn't do it, because I thought that first we should find a relationship between x and the height of mass.

 

[DorelXD]

What you need to connect is x and d. Then you can differentiate the energy equation, and you will obtain the second derivative of d multiplied with the mass; whatever this is equal to is the force.

I don't understand. I must say that my knowledge of calculus is pretty low. Can you explain a little more detalied, please ? What you want me to do is derivate the whole relationship found for energy? :D

The kinetic energy is in the motion of the mass, not in the motion of the ideal massless spring.

Yes, that's what I meant. Sorry for the bad exprimation...:(

 

[voko]

I don't understand. I must say that my knowledge of calculus is pretty low. Can you explain a little more detalied, please ? What you want me to do is derivate the whole relationship found for energy? :D

If you do not understand that, then I suggest we drop this approach. Use the forces.

You still have to find the relationship between $x$ and $d$.

 

[DorelXD]

If you do not understand that, then I suggest we drop this approach. Use the forces.

You still have to find the relationship between $x$ and $d$.

Ok. That's what I've been trying to do. Nothing seems to work. What do you suggest? :)

 

[voko]

Have a look at post #4.

 

[voko]

This drawing might be helpful.

 

[DorelXD]

This drawing might be helpful.

Thank you! Now It begins to make sense. Can you tell me what program did you used for drawing this on a pc? I would like to post better pictures, so that people who answer me can help me much easier.

Well, from now on, I'm going to use the notation on your drawing, because it's very clear and well done.

So, on your drawing , we know that: c + d = constant. But I can't see the displacement of the body. And we need to find a connection between the displacement of the body and the comprimation of the resort, right?

 

[DorelXD]

Oh, wait a minute. Your drawing is for a general state. So let's consider the length a,b,c,d,x for state 1 and a', b',c',d' for state 2. Also let's consider alpha and alpha'

We have that: c + d = c' + d' \to d' - d = y = c - c'
We can easily see that: c = \frac{a -x }{cos{\alpha}} and c' = \frac{a - x' }{cos{\alpha'}}

So, combining the two equations: y =\frac{a - x}{cos{\alpha}} - \frac{a - x' }{cos{\alpha'}}

We also know that the difference \alpha' - \alpha \to 0

Does anything of what I wrote helps in any way :D ?

 

[DorelXD]

I did it!

So y = \frac{a-x}{\cos{\alpha}} - \frac{a-x'}{\cos{\alpha'}} = \frac{a}{\cos{\alpha}} -\frac{x}{\cos{\alpha}} + \frac{a}{\cos{\alpha'}} +\frac{x'}{\cos{\alpha'}}

y = a(\frac{1}{\cos{\alpha}}- \frac{1}{\cos{\alpha'}}) - \frac{x}{\cos{\alpha}} + \frac{x'}{\cos{\alpha'}}

Since alpha is very very close to alpha' we can neglect the term with a and say that: y = - \frac{x}{\cos{\alpha}} + \frac{x'}{\cos{\alpha'}}

Now, we are interested in \Delta x. We write that: x' = \Delta x + x and we substitute in the last realtion found.After a little bit of algebra we will get to:

y\cos{\alpha}\cos{\alpha'} = x ( \cos{\alpha} - \cos{\alpha'} ) + \Delta x \cos{\alpha}

Again, because alpha is very very close to alpha' then aplying the cosine function we will get two values very very close to each other, so we can say that their difference is zero, and hence we can neglect again the first term and say that:

y\cos{\alpha}\cos{\alpha'} = \Delta x \cos{\alpha} which means that: y\cos{\alpha'} = \Delta x

Now, for convenience let's say directly that: y\cos{\alpha'} = x . I know that changing notation in the middle of an exercise isn't a good practice, but in this case, given the fact that I clearly specified what I did, and that I'm not on a contest or test, I'm taking the liberty to do so.

Now, is my reasoning correct? Is this a correct result? I strongly believe that it is. And it's a very beautiful one. Now, please tell me if my work is good, so we can continue with th exercise :D

 

[haruspex]

y = a(\frac{1}{\cos{\alpha}}- \frac{1}{\cos{\alpha'}}) - \frac{x}{\cos{\alpha}} + \frac{x'}{\cos{\alpha'}}

Since alpha is very very close to alpha' we can neglect the term with a

No, you can't do that. x is close to x' in the same order of magnitude, so both terms matter.
Do you know the derivative of sec?

 

[voko]

Can you tell me what program did you used for drawing this on a pc?

I used Inkscape.

So y = \frac{a-x}{\cos{\alpha}} - \frac{a-x'}{\cos{\alpha'}} = \frac{a}{\cos{\alpha}} -\frac{x}{\cos{\alpha}} + \frac{a}{\cos{\alpha'}} +\frac{x'}{\cos{\alpha'}}

y = a(\frac{1}{\cos{\alpha}}- \frac{1}{\cos{\alpha'}}) - \frac{x}{\cos{\alpha}} + \frac{x'}{\cos{\alpha'}}

Since alpha is very very close to alpha' we can neglect the term with a and say that:


y = - \frac{x}{\cos{\alpha}} + \frac{x'}{\cos{\alpha'}}

No, unfortunately you cannot.

But I have a question to ask. Why did you use $(a - x) = c \cos \alpha$ and not $b = c \sin \alpha$? The latter seems a better choice, because it includes only one variable, the angle.

 

[haruspex]

Why did you use $(a - x) = c \cos \alpha$ and not $b = c \sin \alpha$? The latter seems a better choice, because it includes only one variable, the angle.

True, but another equation is needed linking x to alpha, since x is related to the force from the spring. tan(α) looks relevant.

 

[DorelXD]

Ohhh, I now understand that my work was faulty. I cannot say that that difference of cosines is 0. It isn't true.

But I have a question to ask. Why did you use (a−x)=ccosα and not b=csinα? The latter seems a better choice, because it includes only one variable, the angle.

Well I chose the first equation because it contained x, and I couldn't find another link to x. But before using it, I had also thought about the second, but the first won... How do you guys suggest we continue the problem ?

 

[voko]

Is your goal really to retain $x$ in your equations?

Perhaps you should explain first what your general line of attack is. Presumably you want to arrive at some equation - and what variables do you want that equation to have?

 

[DorelXD]

Is your goal really to retain $x$ in your equations?

Perhaps you should explain first what your general line of attack is. Presumably you want to arrive at some equation - and what variables do you want that equation to have?

No, not really. My goal is to write the expression of the resultant force acting on the body. The resultant force depends on the tension, which depends on the elastic force in the spring. I don't know how to continue the problem...

 

[voko]

You can already write the force as suggested by haruspex in #21. But I doubt that will give you the desired result. I believe you really need to think hard what you really want to obtain.

 

[DorelXD]

You can already write the force as suggested by haruspex in #21. But I doubt that will give you the desired result. I believe you really need to think hard what you really want to obtain.

What I want to obtain is that the resultant has the form: R = - ky , that is, it depedns of a constant and of the displacement of the body in raport with its equilbrium position. Is that a good start ?

 

[voko]

Yes, that seems reasonable. Note that means you will need to convert from the angle language to the displacement language. Do you think that keeping $x$ in the mix is helpful along the road?

 

[DorelXD]

Yes, that seems reasonable. Note that means you will need to convert from the angle language to the displacement language. Do you think that keeping $x$ in the mix is helpful along the road?

Not really. But I don't know if we can avoid this. At first, x is gonaa be in the equation of the resultant force but I believe that we will get rid of it because we need to reduce the expression of the force to constant*elongation. So the expression for the force contains only one variable. If we would include x, I mean, if we couldn't get rid of it, we would have two variables, which is not good.

 

[voko]

Again, refer to #21. Can you express the force as a function of the angle?

 

[haruspex]

Not really. But I don't know if we can avoid this. At first, x is gonaa be in the equation of the resultant force but I believe that we will get rid of it because we need to reduce the expression of the force to constant*elongation. So the expression for the force contains only one variable. If we would include x, I mean, if we couldn't get rid of it, we would have two variables, which is not good.

Let's just put together a sufficient set of equations before we worry about which variables to eliminate. Writing
s = relaxed length of spring
x = compression of spring
k = spring constant
α = angle
y = length of hypotenuse
b = vertical distance from pulley to spring
T = tension
m = mass
there are fairly simple equations relating:
1. b, s, x, α
2. T, α, k, x
3. y, b, α
4. T, m, g, $\ddot y$
Four variables, four equations, which in principle can boil down to one variable, one equation. But actually doing that will produce quite a mess, so instead consider perturbations from the equilibrium: ΔT = T - T₀, etc. Note that $\ddot y = \ddot{\Delta y}$.
Even then, you don't need to be too exact. You only need to show that $\ddot{\Delta y}$ ~ $c \Delta y$ for some negative c.