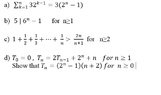Proof Using Induction: Discrete Maths Problem Solving

[Ryuna]

Can someone help me solve the following problems from Discrete Maths, using induction to prove them
View attachment 2554
Thanks in advance

 

[MarkFL]

Hello, and welcome to MHB! :D

In the future, we ask that you post no more than two questions in a thread and that you show what you have tired so we know where you are stuck, and can best help.

I am assuming the first one is instead:

$$\sum_{k=1}^n\left(3\cdot2^{k-1}\right)=3\left(2^n-1\right)$$

The first step is to demonstrate that the base case (for $n=1$) is true. Have you done that?

 

[Ryuna]

^Right, I'll keep that in mind.

And the case is true for n=1. These are practice questions for my exam and I was looking for key answers to use as indicators. I'll be back after trying more.

could you give me a hint on how to start with the last one?

 

[MarkFL]

...could you give me a hint on how to start with the last one?

Well, after showing the base case is true, you want to state your induction hypothesis. It appears to me that using the given recursion will be key to your induction step. I would write the recursion in terms of $n+1$, and see what can be done with that.