- #1
member 731016
- Homework Statement
- I have solved the problem below; however, I am unsure whether it is correct (I list the step below which I am not sure whether I am allowed to do).
- Relevant Equations
- ##M = sup S##
##s > M - \epsilon##
For this problem,
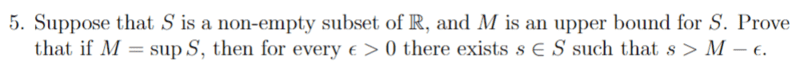
My solution:
Using definition of Supremum,
(a) ##M ≥ s## for all s
(b) ## K ≥ s## for all s implying ##K ≥ M##
##M ≥ s##
##M + \epsilon ≥ s + \epsilon##
##K ≥ s + \epsilon## (Defintion of upper bound)
##K ≥ M ≥ s + \epsilon## (b) in definition of Supremum
##M ≥ s + \epsilon##
Now we have two cases for the inequality:
(1) ##M = s + \epsilon##
(2) ##M > s + \epsilon##
For case (1), ##M ≠ s + \epsilon## from definition of Supremum so,
##M > s + \epsilon##
##M - \epsilon > s##
I am unsure why I get the wrong inequality direction. However, apart for that, it seems correct. I would appreciate any help.
Thanks for any help - Chiral.
My solution:
Using definition of Supremum,
(a) ##M ≥ s## for all s
(b) ## K ≥ s## for all s implying ##K ≥ M##
##M ≥ s##
##M + \epsilon ≥ s + \epsilon##
##K ≥ s + \epsilon## (Defintion of upper bound)
##K ≥ M ≥ s + \epsilon## (b) in definition of Supremum
##M ≥ s + \epsilon##
Now we have two cases for the inequality:
(1) ##M = s + \epsilon##
(2) ##M > s + \epsilon##
For case (1), ##M ≠ s + \epsilon## from definition of Supremum so,
##M > s + \epsilon##
##M - \epsilon > s##
I am unsure why I get the wrong inequality direction. However, apart for that, it seems correct. I would appreciate any help.
Thanks for any help - Chiral.
