Proper Subsets of Ordinals .... .... Another Question .... ....

[Math Amateur]

I am reading Micheal Searcoid's book: "Elements of Abstract Analysis" ... ...

I am currently focused on understanding Chapter 1: Sets ... and in particular Section 1.4 Ordinals ...

I have another question regarding the proof of Theorem 1.4.4 ...

Theorem 1.4.4 reads as follows:

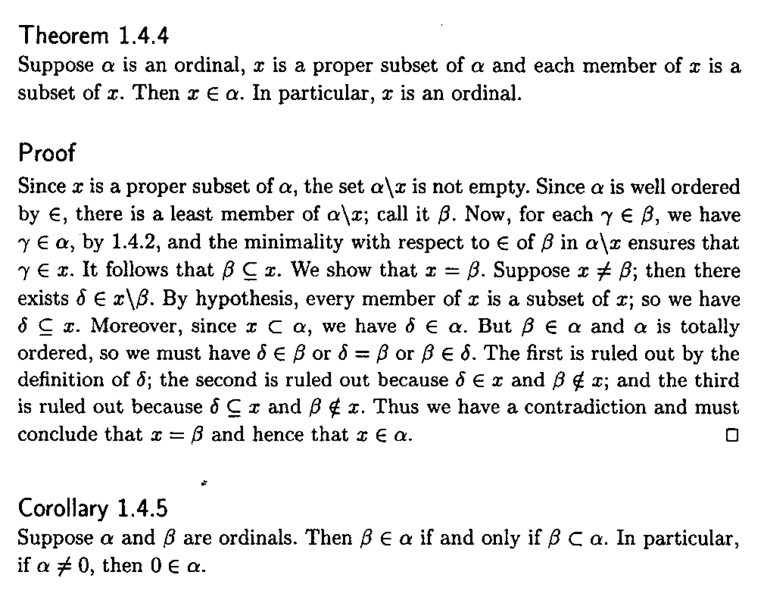In the above proof by Searcoid we read the following:

"... ... Moreover, since $x \subset \alpha$, we have $\delta \in \alpha$. But $\beta \in \alpha$ and $\alpha$ is totally ordered, so we must have $\delta \in \beta$ or $\delta = \beta$ or $\beta \in \delta$ ... ... "My question is regarding the three alternatives $\delta \in \beta$ or $\delta = \beta$ or $\beta \in \delta$ ... ...Now ... where $(S, <)$ is a partially ordered set ... $S$ is said to be totally ordered by $<$ if and only if for every pair of distinct members $x, y \in S$, either $x < y$ or $y < x$ ... ..So if we follow the definition exactly in the quote above there are only two alternatives ... $\delta \in \beta$ or $\beta \in \delta$ ... ...

My question is ... where does the = alternative come from ... ?

How does the = alternative follow from the definition of totally ordered ... ?

Help will be appreciated ...

Peter

 

[andrewkirk]

$S$ is said to be totally ordered by $<$ if and only if for every pair of distinct members $x, y \in S$, either $x < y$ or $y < x$

The key is in the word 'distinct'. The above is equivalent to saying the following, which removes the 'distinct'

$S$ is said to be totally ordered by $<$ if and only if for every pair of members $x, y \in S$, either $x=y$, $x < y$ or $y < x$

Note that, at the stage of the proof where the above words appear, there is nothing to indicate that $\delta$ cannot be the same as $\beta$.

 

[Math Amateur]

The key is in the word 'distinct'. The above is equivalent to saying the following, which removes the 'distinct'Note that, at the stage of the proof where the above words appear, there is nothing to indicate that $\delta$ cannot be the same as $\beta$.

Thanks Andrew ...

Peter