Properties of sequence of random numbers and how to generate random numbers?

[WMDhamnekar]

Hi,
Would any member of Math Help Board explain me the highlighted area in the following paragraphs?

Generating Random Distributions
Now the only missing thing in previous cases is how would one generate a Uniform random, Normal random distributions. We therefore look to cover algorithms to generate such Uniform random distributions and also methods to transform these to other distributions such as Normal Distributions.

The numbers that we will be generating in R for these simulations are actually called pseudorandom numbers which are not truly random but pretty good at mimicking genuine randomness. We generate them using deterministic algorithms such that they approximate the properties of sequence of random numbers.

Uniform Distribution

Uniform Distribution is a continuous distribution abbreviated as U(a,b). Where the probability density function is

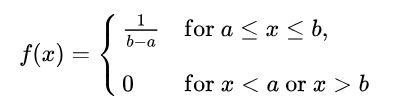The most popular method for generating such numbers is the Linear Congruential Generators. The LCG is generated using-

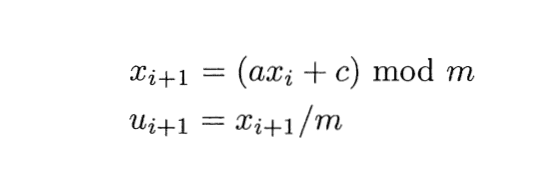
Thus if we choose a x₀ also called the seed. We can generate m-1 unique Uniform Random Numbers between [0,1] . Though a good estimator must follow certain conditions for non zero c.

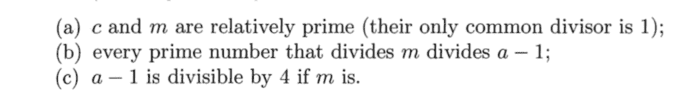
If the above conditions for non-zero c are not fulfilled by a good estimator, what are its effects and results?

 

[Future Bruno]

If the conditions for non-zero c are not fulfilled by a good estimator, it can cause the LCG to generate a small number of distinct values and then repeat those values in a pattern. This would result in a much less random distribution than desired. Additionally, if the values of c, a, and m are not properly chosen, the LCG could produce an output that is not uniform. This means that the probability of some values might be much higher than others, creating an uneven distribution.