Protagonist wants to meet his exact clone

[chasrob]

I’m writing a superhero novel. The protagonist is a normal human transformed (long story) into a super-powered entity. He is similar to Superman in that he has flight, superstrength, superspeed, and is invulnerable, however to an insanely powerful degree. In one chapter he wants to fly to his supposed identical copy, which is 10^(10^29) meters distant (according to Max Tegmark’s article “Parallel Universes”).

This is the large-scale cosmology I invented for the book.

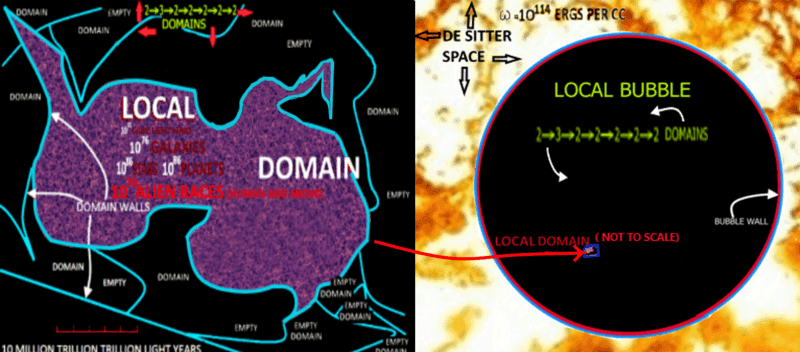
Our “domain” (first drawing) is the space where we occupy and has all the physical constants, etc., to support life, planets, stars, and galaxies. There are 4→7→3→3 (Conway arrow chain) domains like ours (call this number “j”, far larger than Graham's number). It is surrounded by empty domains that have different constants and are therefore empty (they are about the same size, 10^95 cubic light years). There are 2→3→2→2→2→2→2 (“k") of these empty domains, with the “j” domains scattered more or less evenly throughout. All these domains are enclosed in a “local bubble” (second pic). His flight powers are insanely powerful, and he is able to travel throughout the vast “domain” and “local bubble” quickly.

My question (math) is: since the exact clones are so far apart as Tegmark says, and my domains so comparatively small, would by super guy ever come across his identical clone, since they can only exist in "j" domains?

 

[DaveC426913]

I'd be more concerned about how he will find and identify the particular clone that is his exact copy.

The distance to a duplicate is a statistical calculation; it won't tell you where it is. It could, for all you know, be the one right next door (like two aces in a deck being next to each other instead of homogenously distributed).

And how would he know it's the right one? He will pass through innumerable observable universes that are almost identical. Consider the infinite monkeys churning out Hamlet. There will be 130,000 versions churned out that only differ from Hamlet by a single letter. There will be 130,000^2 versions that only differ by two letters, etc. You would have to read every one of them through to the last letter to determine that it's not a duplicate.

So, how long does your hero stick around in a particular OU before he concludes that, in this one his doppleganger wears respectable red socks on Christmas instead of the green socks of a Philistine?

 

[DaveC426913]

And in case that isn't enough of a wrench in your story...

If he is intent on meeting his exact clone, doesn't that mean the clone will come up with the same idea to meet him? Will they fly right past each other on their quests?

Or are they both smart enough to realize that what occurs to me, will occur to my clone, and therefore we would do better to work together. Say, meet in the middle?

Hard to find a middle in an infinite universe. What if we alerted each other where we are? Say, why don't we annihilate a galaxy cluster with antimatter and look for the others' beacon? Hmm. That only works at the speed of light....(Can you tell I just finished reading a novel about infinite alternate worlds? Imagine being the girlfriend of 'Jason' - of which there are infinite copies - all showing up in your universe, all knowing exactly what the others are thinking, all intent on being your 'chosen' one - and willing to kill all the other Jasons to have you?)

 

[chasrob]

Dave, when I said his powers were insane, I meant it :D. He has a reaction time faster than the light travel time across a black hole electron-- 10-66 seconds plus or minus. And he can zip 10^(10^29) meters far faster, since he can visit all "k" domains in a Planck time (one ten millionth of a trillionth of a trillionth of a trillionth of a second).

Your point is very good, but my thoughts are there may be *no* such clones since the "j" domains are not contiguous--he can't go from one "j" to another "j" without crossing a vast chasm of dead and empty domains. That is, 10^31 light years is a lot smaller than 10^(10^29) meters.

That's why I added the "math" tag.

 

[chasrob]

...

Hard to find a middle in an infinite universe. What if we alerted each other where we are? Say, why don't we annihilate a galaxy cluster with antimatter and look for the others' beacon? Hmm. That only works at the speed of light....
...

Wow. Since in my scenario there are on average a couple races, human intelligence and above, in each galaxy, that would be genocide on a massive scale. Luckily, my protag would never do that ;). He retained his scruples from when he was an ordinary Joe.

 

[DaveC426913]

Dave, when I said his powers were insane, I meant it :D. He has a reaction time faster than the light travel time across a black hole electron-- 10-66 seconds plus or minus. And he can zip 10^(10^29) meters far faster, since he can visit all "k" domains in a Planck time (one ten millionth of a trillionth of a trillionth of a trillionth of a second).

Yes. All granted as required for the story.

Your point is very good, but my thoughts are there may be *no* such clones since the "j" domains are not contiguous--he can't go from one "j" to another "j" without crossing a vast chasm of dead and empty domains. That is, 10^31 light years is a lot smaller than 10^(10^29) meters.

None of which changes the problem I pose.

The differences in various locations in this infinite universes are on a continuum. Between every instance of a protagonist, there are vast, vast spaces that are identical except he doesn't exist. Indeed, there are a vast, vast number where humans don't exist. There are vast OUs where Earth doesn't exist. There are vast OUs where planets don't exist.

And they don't come with contents labels. These are not discrete mini-universes. Every shade of likeness possible is there in-between. Places where there are no galaxies. He flies to an arbitrary location in space and looks about and says "Well, I see some stars. A thousand of them are G2, I guess I'll check them out one-by-one to see if they have any planets..."It's as of you think the universes are like words in the story of Hamlet, and you're looking for identical words. That's not the case.

You're looking at an infinite sea of static "snow", and every once in a while, some collection of snow miiiiiiight look a little like a capital T. All the rest of the snow is there that you have to search through.

Search the static for eons and you might find another clump that looks like a capital "T" next to an "a". Search for 13 or 14 more eons, passing by clumps of "Tb", "Tc", "Td", etc and you might stumble across a clump that actually sort of resembles "To".

Search for 26 cubed more aeons and you might find a clump that looks like "To b"

You have 26-to-the-pwer-of-130,000 aeons of searching still ahead of you.

And that's just a simple object.

 

[chasrob]

Seems to me Tegmark's calculation involves a linear distance; an actual minimal distance to the exact clone from the protag. The relevant domain, his/our domain, is a tiny fraction of that distance in extent, and is too far apart from other domains to be affected/influenced, even at light speed. Wouldn't that mean that there are *no* exact copies of the protagonist? Maybe some that are very similar, perhaps a twin in physical form...since there are 10^76 life forms that are human intelligence and above (and it's stipulated that evolution is convergent..

 

[phinds]

I don't see what your problem is. As far as actual science is concerned, your entire scenario is beyond ridiculous so just wave your hands and make it happen.

 

[DaveC426913]

too far apart from other domains to be affected/influenced, even at light speed

Sorry, it goes without saying that Einsteinian physics simply do not apply to your hero.

He can fly trillions of light years in a nanosecond just doing a leisurely backstroke. You stated this at the get-go.

 

[chasrob]

Okay, disregard superguy looking for his exact replica. According to Tegmark's article, if space is an infinite ergodic universe, which contains Hubble volumes realizing all initial conditions, there is an identical copy of you about 10^(10^29) meters away. My crude drawing--

is different, yes? The "Local Domain" is not infinite and is far shorter than 10^(10^29) meters in extent. Therefore there are no identical copies of superguy in that space.

But how about the other ("j" in number) different domains that contain galaxies, stars, life? Since they are individually smaller as well, does that mean no copies in them also? Or could it be, since there are so many domains, there are googolplexes upon googolplexes of identical copies of superguy throughout the vast expanse of the second drawing (the "Local Bubble")?

 

[Rive]

My question (math) is: since the exact clones are so far apart as Tegmark says, and my domains so comparatively small, would by super guy ever come across his identical clone

I hope you are aware that the whole setup is so away from any scientific considerations that the only possible answer can be given is 'as you wanna' do'?

In a little bit more scientific sense, you should just cheat: regardless the whole distance-woodoo the most exact clone would be the one right from the neighbouring multiverse thread: the one which just split away a nanosec before

 

[phinds]

I hope you are aware that the whole setup is so away from any scientific considerations that the only possible answer can be given is 'as you wanna' do'?

See post #8. He does not seem to care for this answer.

 

[DaveC426913]

regardless the whole distance-woodoo the most exact clone would be the one right from the neighbouring multiverse thread: the one which just split away a nanosec before

The premise here has nothing to do with multiple worlds splitting off in time.

The premise is much simpler: if the universe is truly infinite in extent, then it is only a matter of spatial distance before it must repeat. Statistically, we can calculate the average distance that might be at.

 

[Rive]

The premise here

... is the very same world* salad whether you put that 'clone' far away or fold the whole mess into a parallel multiverse (with an optional long path around if you are in the mood for a long walk).
It's just matter of mapping.

(*) ... well, wanted to write 'word' originally, but works both way, actually

 

[PeroK]

The premise here has nothing to do with multiple worlds splitting off in time.

The premise is much simpler: if the universe is truly infinite in extent, then it is only a matter of spatial distance before it must repeat. Statistically, we can calculate the average distance that might be at.

There were two identical cartons of milk right next to each other in the supermarket, so you don't have to go sa far to find a duplicate quart of milk. To find a duplicate planet Earth (whatever that might mean), you'd have to go, I suspect, a practically incalculable distance.

Moreover, that assumes to some extent that there are only finitely many possibilities for a planet. If there are infinitely many possibilities, it's not so clear that each must recur.

 

[DaveC426913]

To find a duplicate planet Earth (whatever that might mean), you'd have to go, I suspect, a practically incalculable distance.

Its been calculated. By Tegmark. Tegmark's article/paper is what spawned the OPs story idea.

I read this article many years ago in SciAm and was similarly intrigued .

*Opinions of SciAm as a source of science notwithstanding.

 

[DaveC426913]

... is the very same world* salad whether you put that 'clone' far away or fold the whole mess into a parallel multiverse (with an optional long path around if you are in the mood for a long walk).
It's just matter of mapping.

But that would be a different story. It is generally considered bad manners to critique a story by saying what you think the story should have been.

The story's in the telling. I'm gonna wait for the author's book signing tour.

(*) ... well, wanted to write 'word' originally, but works both way, actually

Saw that. Well played,sir...

 

[chasrob]

I was just curious as to whether or not my woodoo cosmology and Tegmark’s involved the same distance to the nearest clone. Hmm... Or maybe his claim that the same 100 light year volume as ours would be within 10^(10^91) meters would be a better idea for the superguy since he could cut down the “potential clones” by recognizing star patterns in a galaxy instead of searching every single star in every galaxy. Or maybe I should just forget that chapter and just continue with the chapters about billions of people who want to string the protag up on the nearest tree, because... reasons.

As an aside:
Believe it or not, I roughly based my story’s cosmology (the drawings above) on a paper by a Princeton astrophysicist. That’s where I got the vastly energetic (10^114 Joules per cubic meter) deSitter Space, from which the bubbles were formed 10^-42 s later. I added my domains to his bubbles at the same instant the bubble was formed…not later as Rive said, so there was no waiting involved. Instead of infinite number of bubbles and domains, I instead claimed an immense but finite amount of domains (one of which we and the protag live) in a titanic bubble. Since Gott's deSitter Space is infinite, bubbles would be infinite also, so there would be at least a googolplex factorial superguys, and you and me to contend with. ;)

 

[DaveC426913]

I admit, the inclusion of these domains has gone over my head; I'm going strictly on Tegmark's ideas.

 

[Jarvis323]

in Tegmark's infinite ergodic universe, there would not only be an exact copy of you somewhere in that enormous radius, there would also be an exact copy of you somewhere along a "line" from you in any direction. So if he just set off in any direction and travelled far enough, he would eventually crash right into himself.

 

[PeroK]

Its not only calculable, its been calculated. By Tegmark. Tegmark's article/paper is what spawned the OPs story idea.

This one?

https://space.mit.edu/home/tegmark/PDF/multiverse_sciam.pdf

I'm never convinced by those arguments. Until we have direct evidence of something, it's at best a hypothesis and can never be a certain implication.

 

[DaveC426913]

there would also be an exact copy of you somewhere along a "line" from you in any direction. So if he just set off in any direction and travelled far enough, he would eventually crash right into himself

That's true but it would require ratcheting up the flight speed and perception time from merely 'Ridiculous' to 'Ridiculous to the Power of Ludicrous'.

 

[DaveC426913]

I'm never convinced by those arguments. Until we have direct evidence of something, it's at best a hypothesis and can never be a certain implication.

The article starts with a whopping big "IF" does it not?

And there can be no direct evidence of things causally disconnected from us. Not if Einstein's ghost has anything to say about it.

The OP is writing fiction, whose premise is "what if?"

 

[Jarvis323]

I guess one of the most efficient search methods might be to travel in a line and at each time you intersect a domain like yours, fly around in a space filling curve until you can rule out the universe, and then on to the next one.

If we're talking exact copy down to the last experience, then it likely wouldn't work because your copy would do the same thing, except covering different territory.

I suppose, in Tegmark's infinite ergodic universe, there would also possibly be palindromic chunks of multiverse. But those would be less frequent. If that were the case, it might be possible. Still there would be infinitely many of them. So, exact copies of himself would meet other exact copies. And then they would be stuck in a situation where they mirror each other, moving in the exact same way and saying the exact same thing at the same time.

Otherwise, you could relax the "exactness" constraint and be happy with "similar". Then you need to define similar and redo the math.

Traveling at speeds super-exponentially faster than light would make it hard to see.

 

[DaveC426913]

each time you intersect a domain like yours

Here's my concern: the similarity is a continuum. Its not like there's vacuum between domains and boundaries.

For every volume of space that looks superficially like his target, there are uncountable volumes between that are vaguely like it.

 

[PeroK]

The article starts with a whopping big "IF" does it not?

Not that I can see. It's explicit:

Not just a staple of science fiction, other universes are a direct implication of cosmological observations.

Is there a copy of you reading this article? A person who is not you but who lives on
a planet called Earth, with misty mountains, fertile fields and
sprawling cities, in a solar system with eight other planets? The
life of this person has been identical to yours in every respect.
But perhaps he or she now decides to put down this article with-
out finishing it, while you read on.
The idea of such an alter ego seems strange and implausi-
ble, but it looks as if we will just have to live with it, because it
is supported by astronomical observations.

The underlines are mine. There is no way that is implied by what we observe. There's not even any clear evidence of ET life. Let alone a duplicate Earth.

And there can be no direct evidence of things causally disconnected from us.

That not only casts doubt upon their existence but also raises the question of their reality. The article claims:

This distance is so large that it is beyond astronomical, but that does not make your doppelgänger any less real.

But, something that may or may not exist and that you can never gain any information about cannot be said to be as real as things you have direct information about - like the planet Mars. These duplicate Earths, unlike Mars, are purely hypothetical.

The OP is writing fiction, whose premise is "what if?"

I have no issue with SF.

 

[Jarvis323]

I've not read the SciAm article, but just this one.

The Multiverse Hierarchy
https://arxiv.org/pdf/0905.1283

It may be a better source since it is presented as a research article rather than the SciAm one, which I assume is probably a more sensationalized pop-sci article.

He states that an infinite ergodic universe is a generic prediction of cosmological inflation. Then he seems to just take it as an assumption that the universe is infinite and ergodic and go from there.

 

[DaveC426913]

Not that I can see. It's explicit:

I meant it rhetorically.

It's article premises on IF the universe is infinite in extent. (and, I suppose, homogenous on extremely large scales)

If it is, then it follows that there must be copies - at all degrees of faithfulness - of us.

The calculation is simple. It starts with how many possible configuratioms there are of a given volume of space. I think they were using 100 light years.

The number of configurations is extremely large, but it is not infinite. Therefore it must repeat.

 

[sophiecentaur]

I'd be more concerned about how he will find and identify the particular clone that is his exact copy.

What exactly defines an exact clone?

But that would be a different story. It is generally considered bad manners to critique a story by saying what you think the story should have been.

If anything goes then is there any point in asking for critique of the Science in a story? If it won't work and we ignore that then what was the OP after?

 

[PeroK]

I meant it rhetorically.

It's article premises on IF the universe is infinite in extent. (and, I suppose, homogenous on extremely large scales)

If it is, then it follows that there must be copies - at all degrees of faithfulness - of us.

That's still a conjecture.

The calculation is simple. It starts with how many possible configuratioms there are of a given volume of space. I think they were using 100 light years.

Not all configurations need be equally likely. The required evolution may depend on an uncountable probability space, where events have in fact zero probability.

The number of configurations is extremely large, but it is not infinite. Therefore it must repeat.

Again, that's a conjecture. There's no physical evidence of duplicate Earth's.

 

[DaveC426913]

What exactly defines an exact clone?

That's my point. Its problematic.
For example, he has to stick around at least until Christmas to find out what colour socks this iteration wears.

 

[DaveC426913]

That's still a conjecture.

Yes. This is a what if story. I'm. It not sure what the problem is.

 

[DaveC426913]

Again, that's a conjecture. There's no physical evidence of duplicate Earth's

There's no physical evidence of what's inside the event horizon of a BH either. Does that mean the OP is forbidden fron writing a fictional story about it ?

 

[PeroK]

There's no physical evidence of what's inside the event horizon of a BH either. Does that mean the OP is forbidden fron writing a fictional story about it ?

I was talking about Tegmark's paper, not a SF story.

 

[chasrob]

I just realized--the main character is unique in all multiverses (author fiat) because he was transformed into a super-powered entity. At that moment, he differed from all those copies (I read that there are 10^{10^18} possible life-experiences a person can have, based on a sensory bandwidth of 10¹⁰ bits per second) that were scattered about the multiverse. So, later on when he searches, since there were no exact, identical copies to be found, so he just needs a near copy. Same countenance, age, parents, siblings, friends, etc.